Collective motion and density fluctuations in bacterial colonies
- PMID: 20643957
- PMCID: PMC2922251
- DOI: 10.1073/pnas.1001651107
Collective motion and density fluctuations in bacterial colonies
Abstract
Flocking birds, fish schools, and insect swarms are familiar examples of collective motion that plays a role in a range of problems, such as spreading of diseases. Models have provided a qualitative understanding of the collective motion, but progress has been hindered by the lack of detailed experimental data. Here we report simultaneous measurements of the positions, velocities, and orientations as a function of time for up to a thousand wild-type Bacillus subtilis bacteria in a colony. The bacteria spontaneously form closely packed dynamic clusters within which they move cooperatively. The number of bacteria in a cluster exhibits a power-law distribution truncated by an exponential tail. The probability of finding clusters with large numbers of bacteria grows markedly as the bacterial density increases. The number of bacteria per unit area exhibits fluctuations far larger than those for populations in thermal equilibrium. Such "giant number fluctuations" have been found in models and in experiments on inert systems but not observed previously in a biological system. Our results demonstrate that bacteria are an excellent system to study the general phenomenon of collective motion.
Conflict of interest statement
The authors declare no conflict of interest.
Figures

 ) and a local frame (
) and a local frame ( ) are defined. The cell body and flagella of the ith bacterium are shown by solid and dashed lines, respectively (the flagella are not visible in our images); the local frame is centered at the center of mass
) are defined. The cell body and flagella of the ith bacterium are shown by solid and dashed lines, respectively (the flagella are not visible in our images); the local frame is centered at the center of mass  , with
, with  and
and  pointing at the transverse and longitudinal axes respectively. See
pointing at the transverse and longitudinal axes respectively. See 
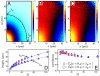
 . In E, values of velocity and orientational correlation at (0,λy) are plotted against n. In D and E, data in blue and red are from Ntotal = 718 and Ntotal = 513, respectively. More cluster-size-dependent correlation functions computed at various conditions can be found in
. In E, values of velocity and orientational correlation at (0,λy) are plotted against n. In D and E, data in blue and red are from Ntotal = 718 and Ntotal = 513, respectively. More cluster-size-dependent correlation functions computed at various conditions can be found in 

 ) against the mean bacterial number N, for interrogation areas of various sizes. Results from three conditions are shown: Ntotal = 343 (squares), Ntotal = 539 (circles), and Ntotal = 718 (triangles). The solid line in B has a slope of 0.25. To obtain the data in B, we define a series of interrogation areas centered at the imaging window with increasing sizes from Ai = 5.4 × 5.4 μm2 to 90 × 90 μm2. We then construct a temporal record of the number of bacteria in each interrogation area Ai (similar to the one in A). From these temporal records, we compute the standard deviation ΔN(Ai) and the mean N(Ai) for each Ai.
) against the mean bacterial number N, for interrogation areas of various sizes. Results from three conditions are shown: Ntotal = 343 (squares), Ntotal = 539 (circles), and Ntotal = 718 (triangles). The solid line in B has a slope of 0.25. To obtain the data in B, we define a series of interrogation areas centered at the imaging window with increasing sizes from Ai = 5.4 × 5.4 μm2 to 90 × 90 μm2. We then construct a temporal record of the number of bacteria in each interrogation area Ai (similar to the one in A). From these temporal records, we compute the standard deviation ΔN(Ai) and the mean N(Ai) for each Ai.References
-
- Parrish JK, Edelstein-Keshet L. Complexity, pattern, and evolutionary trade-offs in animal aggregation. Science. 1999;284:99–101. - PubMed
-
- Buhl J, et al. From disorder to order in marching locusts. Science. 2006;312:1402–1406. - PubMed
-
- Makris NC, et al. Fish population and behavior revealed by instantaneous continental shelf-scale imaging. Science. 2006;311:660–663. - PubMed
-
- Makris NC, et al. Critical population density triggers rapid formation of vast oceanic fish shoals. Science. 2009;323:1734–1737. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

