Effect of electrical double layer on electric conductivity and pressure drop in a pressure-driven microchannel flow

Abstract

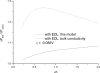
The effect of an electrical double layer (EDL) on microchannel flow has been studied widely, and a constant bulk electric conductivity is often used in calculations of flow rate or pressure drop. In our experimental study of pressure-driven micropipette flows, the pipette diameter is on the same order of magnitude as the Debye length. The overlapping EDL resulted in a much higher electric conductivity, lower streaming potential, and lower electroviscous effect. To elucidate the effect of overlapping EDL, this paper developed a simple model for water flow without salts or dissolved gases (such as CO(2)) inside a two-dimensional microchannel. The governing equations for the flow, the Poisson, and Nernst equations for the electric potential and ion concentrations and the charge continuity equation were solved. The effects of overlapping EDL on the electric conductivity, velocity distribution, and overall pressure drop in the microchannel were quantified. The results showed that the average electric conductivity of electrolyte inside the channel increased significantly as the EDL overlaps. With the modified mean electric conductivity, the pressure drop for the pressure-driven flow was smaller than that without the influence of the EDL on conductivity. The results of this study provide a physical explanation for the observed decrease in electroviscous effect for microchannels when the EDL layers from opposing walls overlap.

Figure 1

Coordinates of parallel microchannel and half channel width is h.

Figure 2

Dimensionless potential distribution in the cross-section of the microchannel. The dimensionless potential and dimensionless channel width are defined by Eqs. 9, 10, and a decreasing κh (the ratio of channel half width to the Debye length) represents increased EDL overlap.

Figure 3

Dimensionless potential at the center of the microchannel at different ratios of channel half width to the Debye length. The exact solution was obtained numerically with no approximations, and the current analytic model neglected the contribution of coions. The semi-infinite model assumed the center of the channel having the condition of bulk water without any effect of EDL overlap.

Figure 4

Average electric conductivity as a function of the ratio of channel half width to the Debye length under different surface zeta potentials.

Figure 5

Velocity distributions across the channel using two different electric conductivity values: bulk water conductivity and the average conductivity accounting EDL overlap. Water velocity distribution without considering EDL effect is also shown as the basis for comparison.

Figure 6

Ratio of pressure drop calculated using the current electric conductivity model and using the electric conductivity of bulk water to the pressure drop calculated without EDL effect.