Applications of a formal approach to decipher discrete genetic networks
- PMID: 20646302
- PMCID: PMC2918581
- DOI: 10.1186/1471-2105-11-385
Applications of a formal approach to decipher discrete genetic networks
Abstract
Background: A growing demand for tools to assist the building and analysis of biological networks exists in systems biology. We argue that the use of a formal approach is relevant and applicable to address questions raised by biologists about such networks. The behaviour of these systems being complex, it is essential to exploit efficiently every bit of experimental information. In our approach, both the evolution rules and the partial knowledge about the structure and the behaviour of the network are formalized using a common constraint-based language.
Results: In this article our formal and declarative approach is applied to three biological applications. The software environment that we developed allows to specifically address each application through a new class of biologically relevant queries. We show that we can describe easily and in a formal manner the partial knowledge about a genetic network. Moreover we show that this environment, based on a constraint algorithmic approach, offers a wide variety of functionalities, going beyond simple simulations, such as proof of consistency, model revision, prediction of properties, search for minimal models relatively to specified criteria.
Conclusions: The formal approach proposed here deeply changes the way to proceed in the exploration of genetic and biochemical networks, first by avoiding the usual trial-and-error procedure, and second by placing the emphasis on sets of solutions, rather than a single solution arbitrarily chosen among many others. Last, the constraint approach promotes an integration of model and experimental data in a single framework.
Figures

 .
.

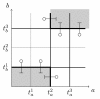
 relative to example in Figure 3.
relative to example in Figure 3.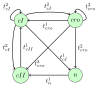
 for the model about immunity control by the λ phage.
for the model about immunity control by the λ phage.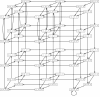
 for the model about carbon nutritional stress in E. coli.
for the model about carbon nutritional stress in E. coli.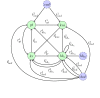
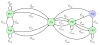
 for the model about gap-gene module of the segmentation of the D. melanogaster embryo.
for the model about gap-gene module of the segmentation of the D. melanogaster embryo.Similar articles
-
Causal Queries from Observational Data in Biological Systems via Bayesian Networks: An Empirical Study in Small Networks.Methods Mol Biol. 2019;1883:111-142. doi: 10.1007/978-1-4939-8882-2_5. Methods Mol Biol. 2019. PMID: 30547398 Review.
-
Formal methods for Hopfield-like networks.Acta Biotheor. 2013 Mar;61(1):21-39. doi: 10.1007/s10441-013-9169-5. Epub 2013 Feb 5. Acta Biotheor. 2013. PMID: 23381497
-
Gene expression complex networks: synthesis, identification, and analysis.J Comput Biol. 2011 Oct;18(10):1353-67. doi: 10.1089/cmb.2010.0118. Epub 2011 May 6. J Comput Biol. 2011. PMID: 21548810
-
IRIS: a method for reverse engineering of regulatory relations in gene networks.BMC Bioinformatics. 2009 Dec 23;10:444. doi: 10.1186/1471-2105-10-444. BMC Bioinformatics. 2009. PMID: 20030818 Free PMC article.
-
Predicting Evolution Using Regulatory Architecture.Annu Rev Biophys. 2020 May 6;49:181-197. doi: 10.1146/annurev-biophys-070317-032939. Epub 2020 Feb 4. Annu Rev Biophys. 2020. PMID: 32040932 Review.
Cited by
-
Molecular mechanisms underlying COPD-muscle dysfunction unveiled through a systems medicine approach.Bioinformatics. 2017 Jan 1;33(1):95-103. doi: 10.1093/bioinformatics/btw566. Epub 2016 Oct 6. Bioinformatics. 2017. PMID: 27794560 Free PMC article.
-
Logical Modeling and Dynamical Analysis of Cellular Networks.Front Genet. 2016 May 31;7:94. doi: 10.3389/fgene.2016.00094. eCollection 2016. Front Genet. 2016. PMID: 27303434 Free PMC article. Review.
-
"Antelope": a hybrid-logic model checker for branching-time Boolean GRN analysis.BMC Bioinformatics. 2011 Dec 22;12:490. doi: 10.1186/1471-2105-12-490. BMC Bioinformatics. 2011. PMID: 22192526 Free PMC article.
-
A Method to Identify and Analyze Biological Programs through Automated Reasoning.NPJ Syst Biol Appl. 2016 Jul 7;2:16010-. doi: 10.1038/npjsba.2016.10. NPJ Syst Biol Appl. 2016. PMID: 27668090 Free PMC article.
-
Formal reasoning about systems biology using theorem proving.PLoS One. 2017 Jul 3;12(7):e0180179. doi: 10.1371/journal.pone.0180179. eCollection 2017. PLoS One. 2017. PMID: 28671950 Free PMC article.
References
-
- Thomas R, D'Ari R. Biological Feedback. CRC Press; 1990.
-
- Corblin F, Bordeaux L, Fanchon E, Hamadi Y, Trilling L. Connections and Integration with SAT Solvers: A Survey and a Case Study in Computational Biology. Hybrid Optimization: the 10 years of CPAIOR, Springer. 2010. in press .
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

