Drug-target residence time: critical information for lead optimization
- PMID: 20663707
- PMCID: PMC2918722
- DOI: 10.1016/j.cbpa.2010.06.176
Drug-target residence time: critical information for lead optimization
Abstract
Failure due to poor in vivo efficacy is a primary contributor to attrition during the development of new chemotherapeutics. Lead optimization programs that in their quest for efficacy focus solely on improving the affinity of drug-target binding are flawed, since this approach ignores the fluctuations in drug concentration that occur in vivo. Instead the lifetime of the drug-target complex must also be considered, since drugs only act when they are bound to their targets. Consequently, to improve the correlation between the in vitro and in vivo activity of drugs, measurements of drug-target residence time must be incorporated into the drug discovery process.
2010 Elsevier Ltd. All rights reserved.
Figures
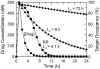

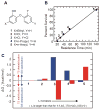
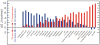
References
-
- Kola I, Landis J. Can the pharmaceutical industry reduce attrition rates? Nat Rev Drug Discov. 2004;3:711–715. - PubMed
-
- Tummino PJ, Copeland RA. Residence time of receptor-ligand complexes and its effect on biological function. Biochemistry. 2008;47:5481–5492. A recent reivew that discusses the differences between closed (in vitro) and open (in vivo) systems, and describes the different mechanisms that underpin slow binding inhibition. This paper also gives examples of long residence time receptor-ligand complexes and discusses the implications of this for drug development. - PubMed
-
- Copeland RA, Pompliano DL, Meek TD. Drug-target residence time and its implications for lead optimization. Nat Rev Drug Discov. 2006;5:730–739. One of the early reviews that discusses the concept of drug-target residence time and the role that long residence time can have on in vivo drug efficacy and target selectivity. This paper also gives examples of drugs that have long residence times on their targets. - PubMed
-
- Swinney DC. The role of binding kinetics in therapeutically useful drug action. Curr Opin Drug Discov Devel. 2009;12:31–39. This paper descibes how drug-target binding kinetics can infuence clinical efficacy, duration of action, clinical differentiation and safety. Based on this, it is proposed that the optimization of binding kinetics can be used to maximize a drug’s therapeutic window and reduce attrition rates. - PubMed
-
- Copeland R. The dynamics of drug-target interactions: drug target residence time and its impact on efficay and safety. Expert Opin Drug Discov. 2010;5:1–6. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

