SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space

Abstract

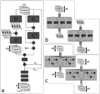
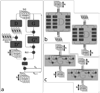
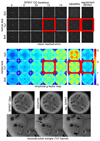
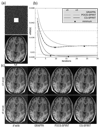
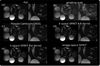
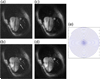
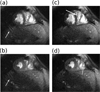
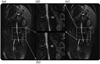
A new approach to autocalibrating, coil-by-coil parallel imaging reconstruction, is presented. It is a generalized reconstruction framework based on self-consistency. The reconstruction problem is formulated as an optimization that yields the most consistent solution with the calibration and acquisition data. The approach is general and can accurately reconstruct images from arbitrary k-space sampling patterns. The formulation can flexibly incorporate additional image priors such as off-resonance correction and regularization terms that appear in compressed sensing. Several iterative strategies to solve the posed reconstruction problem in both image and k-space domain are presented. These are based on a projection over convex sets and conjugate gradient algorithms. Phantom and in vivo studies demonstrate efficient reconstructions from undersampled Cartesian and spiral trajectories. Reconstructions that include off-resonance correction and nonlinear l(1)-wavelet regularization are also demonstrated.

Figure 1

(a) Traditional 2D GRAPPA: Missing k-space data are synthesized from neighboring acquired data. The synthesizing kernel depends on the specific sampling pattern in the neighborhood of the missing point. The reconstruction of a point is independent of the reconstruction of other missing points. (b) Cartesian SPIRiT reconstruction: Three consistency equations are illustrated. The reconstruction of each point on the grid is dependent on its entire neighborhood. The reconstruction of missing points depends on the reconstruction of other missing points. The calibration consistency equation is independent of the sampling pattern. (c) Non-Cartesian SPIRiT: The calibration consistency equation is Cartesian (red). The acquisition data consistency relation between the Cartesian missing points and the non-Cartesian acquired points is shown in blue. These define a large set of linear equations that is sufficient for reconstruction.

Figure 2

k-Space based reconstruction. (a) Illustration of the conjugate-gradient algorithm for non-Cartesian consistency constrained reconstruction in k-space. (b) Illustration of the interpolation operator, D, and its adjoint, D* (c) Illustration of the calibration consistency operator, G and its adjoint, G*. The notation ${\widehat{g}}_{ji}^{*}$ stands for an inverted conjugated version of the filter g_ji.

Figure 3

Image-space based reconstruction. (a) Illustration of the conjugate gradient algorithm for non-Cartesian consistency constrained reconstruction in image space. (b) Illustration of the non-uniform Fourier transform operator, D, and its adjoint, D* (c) Illustration of the calibration consistency operator, G and its adjoint, G*.

Figure 4

Empirical reconstruction error and noise amplification maps of SPIRiT, GRAPPA and ℓ₁-wavelet regularized SPIRiT obtained from 100 scans using 8 channels and 4-fold acceleration (a) The mean residual of SPIRiT as a function of kernel size and number of CG iterations show convergence around 10–12 iterations and overall insensitivity to kernel size. GRAPPA exhibits larger residuals than SPIRiT, especially for smaller kernel sizes. The ℓ₁-wavelet regularization does not reduce the accuracy of the reconstruction (e.g., does not introduce image blurring). (b) The empirical g-factor maps demonstrate the inherent regularization and noise reduction in early termination of CG. SPIRiT exhibits an overall lower noise amplification than GRAPPA for similar residual error. The ℓ₁-wavelet regularization exhibits almost no noise amplification at all. (c) Reconstruction example. The black arrow point to residual aliasing in GRAPPA that is absent in SPIRiT. The arrowheads point to significant noise reduction in the ℓ₁-wavelet regularized SPIRiT.

Figure 5

CG-SPIRiT and POCS-SPIRiT from 3-fold and 5-fold arbitrary Cartesian sampling using 8 channels. (a) 5-fold acceleration poisson-disc density sampling pattern and the reconstruction from the full data (b) Normalized RMSE (nRMSE) as a function of iterations. The advantage of SPIRiT shows at higher acceleration where efficient use of the acquired data becomes crucial. (c) Examples of the various reconstruction. Note the reduction in noise and artifacts in the SPIRiT reconstructions from 5-fold accelerated data.

Figure 6

Non-Cartesian SPIRiT reconstruction from 3-fold undersampled spirals and 4 channels. (a) Reconstruction from fully sampled data. (b) Gridding with density compensation (c) Pseudo-Cartesian GRAPPA /w GROG (d) k-space SPIRiT with Kaiser-Bessel interpolator kernel (e) k-space SPIRiT with flat pass band interpolator kernel (f) Image-space SPIRiT

Figure 7

Dynamic cardiac imaging with dual density spirals with 3-fold acceleration and 4 channels. Two phases of a four chamber view of the heart. (a)–(b) Sum-of-squares of gridding reconstruction exhibits coherent (arrows) and incoherent (noise-like) aliasing artifacts. (c)–(d) Both the coherent and incoherent artifacts are removed by SPIRiT. (e) One out of the three spiral interleaves.

Figure 8

Dynamic cardiac imaging with dual density spirals and off-resonance correction with 3-fold acceleration and 4 channels. Two phases of a short axis view of the heart. (a)–(b) sum-of-squares of gridding reconstruction exhibits coherent (arrows), incoherent (noise-like) aliasing artifacts and blurring due to off-resonance. (c)–(d) SPIRiT reduces both the coherent and incoherent artifacts as well as deblurring the image (arrows).

Figure 9

ℓ₁ wavelet regularization of 4-fold accelerated post-contrast abdomen scan with a 12 channel body coil (a) the non-Regularized GRAPPA reconstruction exhibits noise amplification due to the g factor, especially in the middle of the image. (b) Zoomed in GRAPPA reconstruction. (c) The noise amplification is suppressed in the ℓ₁ wavelet regularized SPIRiT reconstruction, while the edges and features in the image are preserved. (d) Zoomed in ℓ₁ wavelet regularized SPIRiT reconstruction.