Bacterial chemotaxis in linear and nonlinear steady microfluidic gradients

Abstract

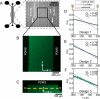
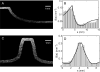
Diffusion-based microfluidic devices can generate steady, arbitrarily shaped chemical gradients without requiring fluid flow and are ideal for studying chemotaxis of free-swimming cells such as bacteria. However, if microfluidic gradient generators are to be used to systematically study bacterial chemotaxis, it is critical to evaluate their performance with actual quantitative chemotaxis tests. We characterize and compare three diffusion-based gradient generators by confocal microscopy and numerical simulations, select an optimal design and apply it to chemotaxis experiments with Escherichia coli in both linear and nonlinear gradients. Comparison of the observed cell distribution along the gradients with predictions from an established mathematical model shows very good agreement, providing the first quantification of chemotaxis of free-swimming cells in steady nonlinear microfluidic gradients and opening the door to bacterial chemotaxis studies in gradients of arbitrary shape.

Figure 1

A,B. Schematic planar layouts of a class of diffusion-based microfluidic gradient generators for (A) linear and (B) nonlinear gradients. Constant-concentration boundary conditions in the source channel (flowing chemoattractant) and sink channel (flowing buffer) generate a steady gradient in the test channel by diffusion through the underlying agarose layer. L is the distance between the ‘feeder’ channels (i.e. source and sink channels), measured between their inner walls facing towards the test channel. The direction of the gradient (s) corresponds to the x axis in this case. C,D. Microdevice to study chemotaxis in linear gradients. (C) micrograph illustrating planar layout (source and sink channels are shown schematically in green and white, respectively) and (D) numerically computed concentration profile across the test channel, for source and sink concentrations of 0.1 and 0 mM, respectively. E–H. Microdevices to study chemotaxis in nonlinear gradients. (E,G) Micrographs showing the planar layout of the microdevices to create an exponential and a peaked concentration profile, respectively. s denotes the coordinate along the test channel. (F,H) Concentration profiles along the channels in E and G, respectively, computed numerically from the shape of the microchannels. The source and sink concentrations were 1 and 0 mM, respectively.

Figure 2

Schematic vertical cross-sections of three different designs of the diffusion-based microfluidic gradient generator. The designs differ in the arrangement of the source, sink and test channels within the agarose and PDMS layers. A. Design1, with all three channels in the PDMS layer. B. Design 2, with all three channels in the agarose layer. C. Design 3, with source and sink channels in the agarose layer, test channel in the PDMS layer. In all designs, the test channel was separated from the feeder (i.e. source and sink) channels by a 200 μm wide layer of PDMS (A,C) or agarose (B), resulting in an edge-to-edge distance between the feeder channels of L = 1 mm. The intensity of the green shading is illustrative of the chemoattractant field in the channels (shown quantitatively in Fig. 4).

Figure 3

A. Planar layout of the microdevice to generate a steady linear gradient (schematic and micrograph). B. Confocal image showing fluorescence at mid-depth in the test channel for the planar section defined by the black box in A. 100 μM fluorescein was added to the source channel (shown in A). C. Vertical line-scan of the test channel taken along the centerline of the same region. The dashed line MN indicates mid-depth and corresponds to the image in B. D–F. Concentration profiles across the width of the test channel, at channel mid-depth, for designs 1 (D), 2 (E), and 3 (F) (see Fig. 2). The green dots are confocal data for fluorescence intensity, obtained along the mid-depth cross-section of each test channel (line MN in C). The red lines are numerically modeled profiles, taken along MN in Fig. 4A–C, respectively. Triangular markers labeled M and N indicate the corresponding points in panel C and Fig. 4A–C. The blue dashed line corresponds to the one-dimensional solution, i.e. the profile predicted if concentration decayed linearly between source and sink. Q_O measures the ratio of the magnitudes of the experimentally observed gradient and the predicted one-dimensional gradient. Q_S measures the ratio of the magnitudes of the numerically computed gradient and the predicted one-dimensional gradient. C(x) represents concentration normalized by the concentration in the source channel.

Figure 4

A–C. Numerically modeled concentration fields in the agarose layer and in the test channel (middle channel in each panel) for designs 1 (A), 2 (B), and 3 (C) (see Fig. 2). Transects EF and MN indicate cross sections at the top of the agarose layer and at mid-depth in the test channel, respectively, and correspond to the numerically modeled concentration profiles plotted in panel D and in Fig. 3D–F, respectively. D. Numerically modeled concentration profiles, C(x), at the top of the agarose layer, along lines EF in panels A–C. Triangular markers labeled E and F indicate the corresponding points in panels A–C. The dashed line is the one-dimensional solution, i.e. the profile predicted if concentration decayed linearly between source (x = -500 μm) and sink (x = 500 μm). These profiles show that the concentration profile in the agarose layer is not linear and that the departure from linearity is design-dependent. In all cases, concentrations were normalized by the concentration in the source channel.

Figure 5

Chemotactic response of the bacteria E. coli to a linear gradient of α-methylaspartate. A constant flow (1 μl/min) was maintained in the source and sink channels, containing 0.1 mM α-methylaspartate and motility buffer, respectively (see Fig. 1C for the microdevice layout). This corresponds to a predicted one-dimensional gradient magnitude G_E = 0.1 mM/mm and an actual gradient magnitude G_O = 0.069 mM/mm (since Q_O = 0.69, see text). A. Long-time-exposure image, recorded over 9.4 s, showing trajectories of E. coli cells. Note the accumulation of cells in the highest concentration region, on the side of the test channel closest to the source channel (left). B. Normalized distribution of E. coli cells along the gradient, B(s), from the experiments (bars) and the numerical model (line). The model result is the solution of the bacterial transport equation (Eqs. 1,2) for μ = 5.9×10^-6 cm² s^-1 and χ₀ = 5.0×10^-4 cm² s^-1. B(s) was normalized so as to have an area of 1.

Figure 6

Response of E. coli to (A,B) an exponential and (C,D) a peaked concentration profile of α-methylaspartate (see Fig. 1E–H for the microdevices’ layout). The concentration of α-methylaspartate in the source and sink channels was 1 and 0 mM, respectively. A,C. Long-time-exposure images of cell trajectories, constructed from a mosaic of 7 (A) and 8 (C) images, each recorded over 6.7 s and acquired in rapid sequence. Accumulation of cells in the highest concentration region is evidenced by the high density of trajectories (white). B,D. Normalized distribution of E. coli cells along the test channel, B(s), from the experiments (bars) and the numerical model (solid line). The model results correspond to the solution of the bacterial transport equation (Eqs. 1,2) for the best-fit values of μ and χ₀. B. μ = 7.0×10^-6 cm² s^-1, χ₀ = 4.5×10^-4 cm² s^-1 D. μ = 7.0×10^-6 cm² s^-1, χ₀ = 4.1×10^-4 cm² s^-1. B(s) was normalized so as to have an area of 1.