Properties of a general PK/PD model of antibody-ligand interactions for therapeutic antibodies that bind to soluble endogenous targets

Abstract

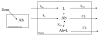
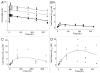
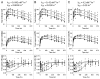
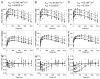
Antibodies that target endogenous soluble ligands are an important class of biotherapeutic agents. While much focus has been placed on characterization of antibody pharmacokinetics, less emphasis has been given to characterization of antibody effects on their soluble targets. We describe here the properties of a generalized mechanism-based PK/PD model used to characterize the in vivo interaction of an antibody and an endogenous soluble ligand. The assumptions and properties of the model are explored, and situations are described when deviations from the basic assumptions may be necessary. This model is most useful for in vivo situations where both antibody and ligand levels are available following drug administration. For a given antibody exposure, the extent and duration of suppression of free ligand is impacted by the apparent affinity of the interaction, as well as by the rate of ligand turnover. The applicability of the general equilibrium model of in vivo antibody-ligand interaction is demonstrated with an anti-Aß antibody.

Figure 1

Schematic diagram of the basic equilibrium model. Ab represents antibody concentration; k_a is a 1^st-order absorption rate constant for the antibody; V is the apparent volume of distribution for the antibody; CL is the apparent clearance for the antibody; L is free ligand concentration; k_in is a zero-order input rate constant for ligand (units of concentration/time); k_out is a 1^st-order rate constant for free ligand elimination; K_D is the equilibrium constant governing antibody-ligand binding; Ab•L is concentration of antibody-ligand complex.

Figure 2

Simulations illustrating effects of varying K_D in the general antibody-ligand PK/PD model. All parameters except K_D were held constant throughout simulations. K_D was 0.1, 1 and 10 nM for the three scenarios. Effect of varying K_D on total antibody concentration (A–C), total ligand (D–F) and free ligand (G–I) are shown. (J–L) show total antibody, total ligand and free ligand on the same plot for each scenario at a 100 mg/kg dose of antibody.

Figure 3

Simulations illustrating effect of varying k_in and k_out in the general antibody-ligand PK/PD model. All parameters except k_in and k_out were held constant throughout simulations and the ratio of k_in to k_out was held constant at 0.061. k_in was 0.42, 0.042 and 0.0042 nM h⁻¹ for the three scenarios. Effect of varying k_in and k_out on total antibody concentration (A–C), total ligand concentration (D–F) and free ligand concentration (G–I) are shown. (J–L) show total antibody, total ligand and free ligand concentrations on the same plot for each scenario at a 100 mg/kg dose of antibody.

Figure 4

Observed and model predicted antibody and ligand (Aβ_1–40) levels obtained using the general equilibrium model to fit m266 PK and ligand data in the PDAPP mouse. Symbols represent individual animal data and lines are population means for doses of 0.5 (●, —), 2 (○, ⋯) and 5 (●, ---) mg/kg of antibody. Antibody concentrations are shown in (A) with total ligand concentrations following 0.5, 2 and 5 mg/kg m266 shown in (B–D) respectively.

Figure 5

Antibody and ligand levels obtained by simulation using the non-equilibrium model (symbols) for 3 k_on/k_off scenarios compared with simulations obtained using the equilibrium model (lines). All parameters except k_on and k_off were held constant throughout simulations and the ratio of k_off and k_on was held constant at 0.03 nM. Symbols and lines are population means for n = 4 for doses of 0.5 (●, —), 1.5 (▼, ···) and 5 (■, ---) mg/kg of antibody. Vehicle control is also shown for the free ligand plots (-●-). Total antibody concentrations (A–C), free antibody concentrations (D–F), total ligand concentrations (G–I) and free ligand concentrations (J–L) are shown.

Figure 6

Total antibody (A–C) and total ligand (D–F) concentrations for 3 k_on/k_off scenarios fitted to the equilibrium model. Symbols represent simulated data used for fitting and lines represent model predicted means for doses of 0.5 (●, —), 1.5 (△, ⋯) and 5 (◆, ---) mg/kg of antibody. Plots in (G–I) illustrate comparison between simulated data and model predicted mean free ligand concentrations.

Figure 7

Total antibody (A–C), total ligand (D–F) and free ligand (G–I) concentrations for 3 k_on/k_off scenarios fitted simultaneously to the equilibrium model. Symbols represent simulated data used for fitting and lines represent model predicted means for doses of 0.5 (●, —), 1.5 (△, ⋯) and 5 (◆, ---) mg/kg of antibody.