Hashing algorithms and data structures for rapid searches of fingerprint vectors
- PMID: 20681581
- PMCID: PMC2926297
- DOI: 10.1021/ci100132g
Hashing algorithms and data structures for rapid searches of fingerprint vectors
Abstract
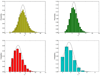
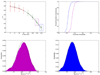
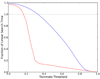
In many large chemoinformatics database systems, molecules are represented by long binary fingerprint vectors whose components record the presence or absence of particular functional groups or combinatorial features. To speed up database searches, we propose to add to each fingerprint a short signature integer vector of length M. For a given fingerprint, the i component of the signature vector counts the number of 1-bits in the fingerprint that fall on components congruent to i modulo M. Given two signatures, we show how one can rapidly compute a bound on the Jaccard-Tanimoto similarity measure of the two corresponding fingerprints, using the intersection bound. Thus, these signatures allow one to significantly prune the search space by discarding molecules associated with unfavorable bounds. Analytical methods are developed to predict the resulting amount of pruning as a function of M. Data structures combining different values of M are also developed together with methods for predicting the optimal values of M for a given implementation. Simulations using a particular implementation show that the proposed approach leads to a 1 order of magnitude speedup over a linear search and a 3-fold speedup over a previous implementation. All theoretical results and predictions are corroborated by large-scale simulations using molecules from the ChemDB. Several possible algorithmic extensions are discussed.
Figures




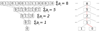
Similar articles
-
Speeding up chemical database searches using a proximity filter based on the logical exclusive or.J Chem Inf Model. 2008 Jul;48(7):1367-78. doi: 10.1021/ci800076s. Epub 2008 Jul 2. J Chem Inf Model. 2008. PMID: 18593143
-
Tree and Hashing Data Structures to Speed up Chemical Searches: Analysis and Experiments.Mol Inform. 2011 Sep;30(9):791-800. doi: 10.1002/minf.201100089. Epub 2011 Sep 5. Mol Inform. 2011. PMID: 27467411
-
An intersection inequality sharper than the tanimoto triangle inequality for efficiently searching large databases.J Chem Inf Model. 2009 Aug;49(8):1866-70. doi: 10.1021/ci900133j. J Chem Inf Model. 2009. PMID: 19601605 Free PMC article.
-
Data-driven high-throughput prediction of the 3-D structure of small molecules: review and progress.J Chem Inf Model. 2011 Apr 25;51(4):760-76. doi: 10.1021/ci100223t. Epub 2011 Mar 18. J Chem Inf Model. 2011. PMID: 21417267 Free PMC article. Review.
-
Basic overview of chemoinformatics.J Chem Inf Model. 2006 Nov-Dec;46(6):2267-77. doi: 10.1021/ci600234z. J Chem Inf Model. 2006. PMID: 17125169 Review.
Cited by
-
The chemfp project.J Cheminform. 2019 Dec 5;11(1):76. doi: 10.1186/s13321-019-0398-8. J Cheminform. 2019. PMID: 33430977 Free PMC article.
-
Methods for Similarity-based Virtual Screening.Comput Struct Biotechnol J. 2013 Mar 3;5:e201302009. doi: 10.5936/csbj.201302009. eCollection 2013. Comput Struct Biotechnol J. 2013. PMID: 24688702 Free PMC article. Review.
-
Speeding up chemical searches using the inverted index: the convergence of chemoinformatics and text search methods.J Chem Inf Model. 2012 Apr 23;52(4):891-900. doi: 10.1021/ci200552r. Epub 2012 Apr 10. J Chem Inf Model. 2012. PMID: 22462644 Free PMC article.
References
-
- Chen J, Swamidass SJ, Dou Y, Bruand J, Baldi P. ChemDB: a public database of small molecules and related chemoinformatics resources. Bioinformatics. 2005;21:4133–4139. - PubMed
-
- Chen J, Linstead E, Swamidass SJ, Wang D, Baldi P. ChemDB Update–Full Text Search and Virtual Chemical Space. Bioinformatics. 2007;23:2348–2351. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

