Pattern separation in the dentate gyrus: a role for the CA3 backprojection
- PMID: 20683841
- PMCID: PMC2976779
- DOI: 10.1002/hipo.20828
Pattern separation in the dentate gyrus: a role for the CA3 backprojection
Abstract
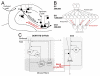
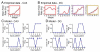
Many theories of hippocampal function assume that area CA3 of hippocampus is capable of performing rapid pattern storage, as well as pattern completion when a partial version of a familiar pattern is presented, and that the dentate gyrus (DG) is a preprocessor that performs pattern separation, facilitating storage and recall in CA3. The latter assumption derives partly from the anatomical and physiological properties of DG. However, the major output of DG is from a large number of DG granule cells to a smaller number of CA3 pyramidal cells, which potentially negates the pattern separation performed in the DG. Here, we consider a simple CA3 network model, and consider how it might interact with a previously developed computational model of the DG. The resulting "standard" DG-CA3 model performs pattern storage and completion well, given a small set of sparse, randomly derived patterns representing entorhinal input to the DG and CA3. However, under many circumstances, the pattern separation achieved in the DG is not as robust in CA3, resulting in a low storage capacity for CA3, compared to previous mathematical estimates of the storage capacity for an autoassociative network of this size. We also examine an often-overlooked aspect of hippocampal anatomy that might increase functionality in the combined DG-CA3 model. Specifically, axon collaterals of CA3 pyramidal cells project "back" to the DG ("backprojections"), exerting inhibitory effects on granule cells that could potentially ensure that different subpopulations of granule cells are recruited to respond to similar patterns. In the model, addition of such backprojections improves both pattern separation and storage capacity. We also show that the DG-CA3 model with backprojections provides a better fit to empirical data than a model without backprojections. Therefore, we hypothesize that CA3 backprojections might play an important role in hippocampal function.
Copyright © 2010 Wiley Periodicals, Inc.
Figures



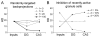


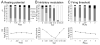


Similar articles
-
Corruption of the dentate gyrus by "dominant" granule cells: Implications for dentate gyrus function in health and disease.Neurobiol Learn Mem. 2016 Mar;129:69-82. doi: 10.1016/j.nlm.2015.09.005. Epub 2015 Sep 29. Neurobiol Learn Mem. 2016. PMID: 26391451 Free PMC article. Review.
-
Function of local circuits in the hippocampal dentate gyrus-CA3 system.Neurosci Res. 2019 Mar;140:43-52. doi: 10.1016/j.neures.2018.11.003. Epub 2018 Nov 5. Neurosci Res. 2019. PMID: 30408501 Review.
-
Impairment of Pattern Separation of Ambiguous Scenes by Single Units in the CA3 in the Absence of the Dentate Gyrus.J Neurosci. 2020 Apr 29;40(18):3576-3590. doi: 10.1523/JNEUROSCI.2596-19.2020. Epub 2020 Mar 31. J Neurosci. 2020. PMID: 32234778 Free PMC article.
-
Dentate Gyrus Mossy Cells Share a Role in Pattern Separation with Dentate Granule Cells and Proximal CA3 Pyramidal Cells.J Neurosci. 2019 Nov 27;39(48):9570-9584. doi: 10.1523/JNEUROSCI.0940-19.2019. Epub 2019 Oct 22. J Neurosci. 2019. PMID: 31641051 Free PMC article.
-
CA3 retrieves coherent representations from degraded input: direct evidence for CA3 pattern completion and dentate gyrus pattern separation.Neuron. 2014 Jan 22;81(2):416-27. doi: 10.1016/j.neuron.2013.11.017. Neuron. 2014. PMID: 24462102 Free PMC article.
Cited by
-
Altered connectomes of adult-born granule cells following engraftment of GABAergic progenitors in the mouse hippocampus.Prog Neurobiol. 2023 Jul;226:102450. doi: 10.1016/j.pneurobio.2023.102450. Epub 2023 Apr 13. Prog Neurobiol. 2023. PMID: 37061022 Free PMC article.
-
Assessments of dentate gyrus function: discoveries and debates.Nat Rev Neurosci. 2023 Aug;24(8):502-517. doi: 10.1038/s41583-023-00710-z. Epub 2023 Jun 14. Nat Rev Neurosci. 2023. PMID: 37316588 Free PMC article. Review.
-
Regulation of dentate gyrus pattern separation by hilus ectopic granule cells.Cogn Neurodyn. 2025 Dec;19(1):10. doi: 10.1007/s11571-024-10204-y. Epub 2025 Jan 9. Cogn Neurodyn. 2025. PMID: 39801911
-
The dynamic impact of adult neurogenesis on pattern separation within the dentate gyrus neural network.Cogn Neurodyn. 2025 Dec;19(1):57. doi: 10.1007/s11571-025-10244-y. Epub 2025 Apr 4. Cogn Neurodyn. 2025. PMID: 40191172
-
Running Changes the Brain: the Long and the Short of It.Physiology (Bethesda). 2017 Nov;32(6):410-424. doi: 10.1152/physiol.00017.2017. Physiology (Bethesda). 2017. PMID: 29021361 Free PMC article. Review.
References
-
- Alle H, Geiger JR. Combined analog and action potential coding in hippocampal mossy fibers. Science. 2006;311:1290–1293. - PubMed
-
- Amaral DG, Ishizuka N, Claiborne B. Neurons, numbers and the hippocampal network. In: Storm-Mathisen J, Zimmer J, Ottersen OP, editors. Understanding the brain through the hippocampus. Elsevier Science; New York, NY: 1990. pp. 1–11. - PubMed
-
- Amaral DG, Lavenex P. Hippocampal neuroanatomy. In: Andersen P, Morris R, Amaral D, Bliss T, O'Keefe J, editors. The Hippocampus Book. Oxford University Press; Oxford, UK: 2007. pp. 37–114.
-
- Amaral DG, Witter MP. The three-dimensional organization of the hippocampal formation: A review of anatomical data. Neuroscience. 1989;31:571–591. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

