Derivation of a finite-element model of lingual deformation during swallowing from the mechanics of mesoscale myofiber tracts obtained by MRI
- PMID: 20689096
- PMCID: PMC2980378
- DOI: 10.1152/japplphysiol.00493.2010
Derivation of a finite-element model of lingual deformation during swallowing from the mechanics of mesoscale myofiber tracts obtained by MRI
Abstract
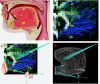
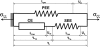
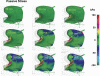
To demonstrate the relationship between lingual myoarchitecture and mechanics during swallowing, we performed a finite-element (FE) simulation of lingual deformation employing mesh aligned with the vector coordinates of myofiber tracts obtained by diffusion tensor imaging with tractography in humans. Material properties of individual elements were depicted in terms of Hill's three-component phenomenological model, assuming that the FE mesh was composed of anisotropic muscle and isotropic connective tissue. Moreover, the mechanical model accounted for elastic constraints by passive and active elements from the superior and inferior directions and the effect of out-of-plane muscles and connective tissue. Passive bolus effects were negligible. Myofiber tract activation was simulated over 500 ms in 1-ms steps following lingual tip association with the hard palate and incorporated specifically the accommodative and propulsive phases of the swallow. Examining the displacement field, active and passive muscle stress, elemental stretch, and strain rate relative to changes of global shape, we demonstrate that lingual reconfiguration during these swallow phases is characterized by (in sequence) the following: 1) lingual tip elevation and shortening in the anterior-posterior direction; 2) inferior displacement related to hyoglossus contraction at its inferior-most position; and 3) dominant clockwise rotation related to regional contraction of the genioglossus and contraction of the hyoglossus following anterior displacement. These simulations demonstrate that lingual deformation during the indicated phases of swallowing requires temporally patterned activation of intrinsic and extrinsic muscles and delineate a method to ascertain the mechanics of normal and pathological swallowing.
Figures
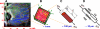




Similar articles
-
Two dimensional computational model coupling myoarchitecture-based lingual tissue mechanics with liquid bolus flow during oropharyngeal swallowing.Comput Biol Med. 2022 Jun;145:105446. doi: 10.1016/j.compbiomed.2022.105446. Epub 2022 Mar 25. Comput Biol Med. 2022. PMID: 35390748
-
Associating the mesoscale fiber organization of the tongue with local strain rate during swallowing.J Biomech. 2008;41(8):1782-9. doi: 10.1016/j.jbiomech.2008.01.030. Epub 2008 May 5. J Biomech. 2008. PMID: 18456271
-
Biomechanical basis for lingual muscular deformation during swallowing.Am J Physiol. 1999 Sep;277(3):G695-701. doi: 10.1152/ajpgi.1999.277.3.G695. Am J Physiol. 1999. PMID: 10484396
-
Anatomical basis of lingual hydrostatic deformation.J Exp Biol. 2007 Dec;210(Pt 23):4069-82. doi: 10.1242/jeb.007096. J Exp Biol. 2007. PMID: 18025008 Review.
-
Contemporary image-based methods for measuring passive mechanical properties of skeletal muscles in vivo.J Appl Physiol (1985). 2019 May 1;126(5):1454-1464. doi: 10.1152/japplphysiol.00672.2018. Epub 2018 Sep 20. J Appl Physiol (1985). 2019. PMID: 30236053 Free PMC article. Review.
Cited by
-
Personalized biomechanical tongue models based on diffusion-weighted MRI and validated using optical tracking of range of motion.Biomech Model Mechanobiol. 2021 Jun;20(3):1101-1113. doi: 10.1007/s10237-021-01435-7. Epub 2021 Mar 7. Biomech Model Mechanobiol. 2021. PMID: 33682028 Free PMC article.
-
How Do Orodispersible Tablets Behave in an In Vitro Oral Cavity Model: A Pilot Study.Pharmaceutics. 2020 Jul 9;12(7):651. doi: 10.3390/pharmaceutics12070651. Pharmaceutics. 2020. PMID: 32660030 Free PMC article.
-
Patterns of intersecting fiber arrays revealed in whole muscle with generalized Q-space imaging.Biophys J. 2015 Jun 2;108(11):2740-9. doi: 10.1016/j.bpj.2015.03.061. Biophys J. 2015. PMID: 26039175 Free PMC article.
-
Fibre and extracellular matrix contributions to passive forces in human skeletal muscles: An experimental based constitutive law for numerical modelling of the passive element in the classical Hill-type three element model.PLoS One. 2019 Nov 5;14(11):e0224232. doi: 10.1371/journal.pone.0224232. eCollection 2019. PLoS One. 2019. PMID: 31689322 Free PMC article.
-
Upper Airway Elasticity Estimation in Pediatric Down Syndrome Sleep Apnea Patients Using Collapsible Tube Theory.Ann Biomed Eng. 2016 May;44(5):1538-52. doi: 10.1007/s10439-015-1430-4. Epub 2015 Aug 28. Ann Biomed Eng. 2016. PMID: 26314989 Free PMC article.
References
-
- Bathe KJ. Finite Element Procedures. Englewood Cliffs, NJ: Prentice-Hall, 1996
-
- Doran GA. Review of the evolution and phylogeny of the mammalian tongue. Acta Anat (Basel) 91: 118–129, 1975 - PubMed
-
- Felton SM, Gaige TA, Benner T, Wang R, Wedeen VJ, Reese TG, Gilbert RJ. Association of mesoscale myofiber architecture with local strain rate during the propulsive phase of human swallowing. J Biomech 41: 1782–1789, 2008 - PubMed
-
- Felton SM, Gaige TA, Reese TG, Wedeen VJ, Gilbert RJ. Mechanical basis for lingual deformation during the propulsive phase of swallowing as determined by phase-contrast magnetic resonance imaging. J Appl Physiol 103: 255–265, 2007 - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

