Spatio-temporal dynamics in fMRI recordings revealed with complex independent component analysis
- PMID: 20689619
- PMCID: PMC2916201
- DOI: 10.1016/j.neucom.2005.12.029
Spatio-temporal dynamics in fMRI recordings revealed with complex independent component analysis
Abstract
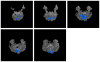
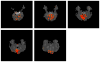
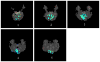
Independent component analysis (ICA) of functional magnetic resonance imaging (fMRI) data is commonly carried out under the assumption that each source may be represented as a spatially fixed pattern of activation, which leads to the instantaneous mixing model. To allow modeling patterns of spatio-temporal dynamics, in particular, the flow of oxygenated blood, we have developed a convolutive ICA approach: spatial complex ICA applied to frequency-domain fMRI data. In several frequency-bands, we identify components pertaining to activity in primary visual cortex (V1) and blood supply vessels. One such component, obtained in the 0.10 Hz band, is analyzed in detail and found to likely reflect flow of oxygenated blood in V1.
Figures



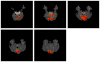
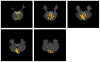

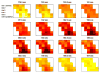


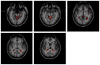
Similar articles
-
Complex independent component analysis of frequency-domain electroencephalographic data.Neural Netw. 2003 Nov;16(9):1311-23. doi: 10.1016/j.neunet.2003.08.003. Neural Netw. 2003. PMID: 14622887 Free PMC article.
-
Gaussian process based independent analysis for temporal source separation in fMRI.Neuroimage. 2017 May 15;152:563-574. doi: 10.1016/j.neuroimage.2017.02.070. Epub 2017 Feb 27. Neuroimage. 2017. PMID: 28249758
-
Analysis of fMRI data by blind separation of data in a tiny spatial domain into independent temporal component.Brain Topogr. 2003 Summer;15(4):223-32. doi: 10.1023/a:1023958024689. Brain Topogr. 2003. PMID: 12866826
-
Spatial and temporal independent component analysis of functional MRI data containing a pair of task-related waveforms.Hum Brain Mapp. 2001 May;13(1):43-53. doi: 10.1002/hbm.1024. Hum Brain Mapp. 2001. PMID: 11284046 Free PMC article.
-
In Vivo Observations of Rapid Scattered Light Changes Associated with Neurophysiological Activity.In: Frostig RD, editor. In Vivo Optical Imaging of Brain Function. 2nd edition. Boca Raton (FL): CRC Press/Taylor & Francis; 2009. Chapter 5. In: Frostig RD, editor. In Vivo Optical Imaging of Brain Function. 2nd edition. Boca Raton (FL): CRC Press/Taylor & Francis; 2009. Chapter 5. PMID: 26844322 Free Books & Documents. Review.
Cited by
-
Utility of independent component analysis for interpretation of intracranial EEG.Front Hum Neurosci. 2010 Nov 2;4:184. doi: 10.3389/fnhum.2010.00184. eCollection 2010. Front Hum Neurosci. 2010. PMID: 21152349 Free PMC article.
-
Reactivity of hemodynamic responses and functional connectivity to different states of alpha synchrony: a concurrent EEG-fMRI study.Neuroimage. 2010 Oct 1;52(4):1252-60. doi: 10.1016/j.neuroimage.2010.05.053. Epub 2010 May 25. Neuroimage. 2010. PMID: 20510374 Free PMC article.
-
Propagations of spontaneous brain activity in awake rats.Neuroimage. 2019 Nov 15;202:116176. doi: 10.1016/j.neuroimage.2019.116176. Epub 2019 Sep 9. Neuroimage. 2019. PMID: 31513942 Free PMC article.
-
Temporal dynamics of perisylvian activation during language processing in children and adults.Neuroimage. 2008 Jul 15;41(4):1484-92. doi: 10.1016/j.neuroimage.2008.03.027. Epub 2008 Mar 28. Neuroimage. 2008. PMID: 18479941 Free PMC article.
-
Independent component analysis applied to the removal of motion artifacts from electrocardiographic signals.Med Biol Eng Comput. 2008 Mar;46(3):251-61. doi: 10.1007/s11517-007-0293-8. Epub 2007 Dec 7. Med Biol Eng Comput. 2008. PMID: 18064502
References
-
- Amari S, Cichocki A, Yang HH. A new learning algorithm for blind signal separation. In: Touretzky D, Mozer M, Hasselmo M, editors. Advances in Neural Information Processing Systems. Vol. 8. MIT Press; Cambridge, MA: 1996. pp. 757–763.
-
- Anemüller J. PhD Thesis. Department of Physics, University of Oldenburg; Oldenburg, Germany: 2001. Across-frequency processing in convolutive blind source separation.
-
- Anemüller J, Gramß T. On-line blind separation of moving sound sources. In: Cardoso JF, Jutten Ch, Loubaton Ph, editors. Proceedings of the First International Workshop on Independent Component Analysis and Blind Signal Separation. Aussois, France: 1999. pp. 331–334.
-
- Anemüller J, Kollmeier B. Adaptive separation of acoustic sources for anechoic conditions: a constrained frequency domain approach. Speech Commun. 2003;39(1–2):79–95.
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
