Modeling of the human skull in EEG source analysis
- PMID: 20690140
- PMCID: PMC6869856
- DOI: 10.1002/hbm.21114
Modeling of the human skull in EEG source analysis
Abstract
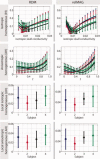
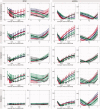
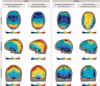
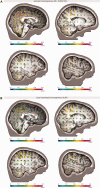
We used computer simulations to investigate finite element models of the layered structure of the human skull in EEG source analysis. Local models, where each skull location was modeled differently, and global models, where the skull was assumed to be homogeneous, were compared to a reference model, in which spongy and compact bone were explicitly accounted for. In both cases, isotropic and anisotropic conductivity assumptions were taken into account. We considered sources in the entire brain and determined errors both in the forward calculation and the reconstructed dipole position. Our results show that accounting for the local variations over the skull surface is important, whereas assuming isotropic or anisotropic skull conductivity has little influence. Moreover, we showed that, if using an isotropic and homogeneous skull model, the ratio between skin/brain and skull conductivities should be considerably lower than the commonly used 80:1. For skull modeling, we recommend (1) Local models: if compact and spongy bone can be identified with sufficient accuracy (e.g., from MRI) and their conductivities can be assumed to be known (e.g., from measurements), one should model these explicitly by assigning each voxel to one of the two conductivities, (2) Global models: if the conditions of (1) are not met, one should model the skull as either homogeneous and isotropic, but with considerably higher skull conductivity than the usual 0.0042 S/m, or as homogeneous and anisotropic, but with higher radial skull conductivity than the usual 0.0042 S/m and a considerably lower radial:tangential conductivity anisotropy than the usual 1:10.
Copyright © 2010 Wiley-Liss, Inc.
Figures

References
-
- Akhtari M, Bryant HC, Marnelak AN, Flynn ER, Heller L, Shih JJ, Mandelkern M, Matlachov A, Ranken DM, Best ED, DiMauro MA, Lee RR, Sutherling WW ( 2002): Conductivities of three‐layer live human skull. Brain Topography 14: 151–167. - PubMed
-
- Awada KA, Jackson DR, Williams JT, Wilton DR, Baumann SB, Papanicolaou AC ( 1997): Computational aspects of finite element modeling in EEG source localization. IEEE Trans Biomed Eng 44: 736–752. - PubMed
-
- Baysal U, Haueisen J ( 2004): Use of a priori information in estimating tissue resistivities—Application to human data in vivo. Physiol Meas 25: 737–748. - PubMed
-
- Bertrand O (1991): 3D Finite element method in brain electrical activity studies. In Nenonen J, Rajala HM, Katila T. (Eds.) (1991): Biomegnetic localization and 3D Modeling, pp. 154–171, Helsinki University of Technology, Helsinki, Finnland.
-
- Braess D (2007): Finite Elements: Theory, Fast Solvers, and Applications in Solid Mechanics, Cambridge University Press; 3 edition (April 30, 2007), ISBN‐10: 0521705185, ISBN‐13: 978‐0521705189.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

