Finite element model of polar growth in pollen tubes
- PMID: 20699395
- PMCID: PMC2947179
- DOI: 10.1105/tpc.110.075754
Finite element model of polar growth in pollen tubes
Abstract
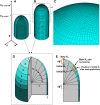
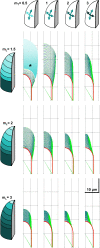
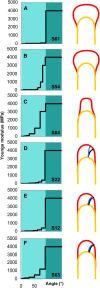
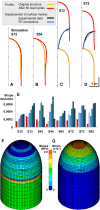
Cellular protuberance formation in walled cells requires the local deformation of the wall and its polar expansion. In many cells, protuberance elongation proceeds by tip growth, a growth mechanism shared by pollen tubes, root hairs, and fungal hyphae. We established a biomechanical model of tip growth in walled cells using the finite element technique. We aimed to identify the requirements for spatial distribution of mechanical properties in the cell wall that would allow the generation of cellular shapes that agree with experimental observations. We based our structural model on the parameterized description of a tip-growing cell that allows the manipulation of cell size, shape, cell wall thickness, and local mechanical properties. The mechanical load was applied in the form of hydrostatic pressure. We used two validation methods to compare different simulations based on cellular shape and the displacement of surface markers. We compared the resulting optimal distribution of cell mechanical properties with the spatial distribution of biochemical cell wall components in pollen tubes and found remarkable agreement between the gradient in mechanical properties and the distribution of deesterified pectin. Use of the finite element method for the modeling of nonuniform growth events in walled cells opens future perspectives for its application to complex cellular morphogenesis in plants.
Figures



Similar articles
-
Persistent symmetry frustration in pollen tubes.PLoS One. 2012;7(11):e48087. doi: 10.1371/journal.pone.0048087. Epub 2012 Nov 5. PLoS One. 2012. PMID: 23144847 Free PMC article.
-
Polar growth in pollen tubes is associated with spatially confined dynamic changes in cell mechanical properties.Dev Biol. 2009 Oct 15;334(2):437-46. doi: 10.1016/j.ydbio.2009.07.044. Epub 2009 Aug 8. Dev Biol. 2009. PMID: 19666018
-
Shape and dynamics of tip-growing cells.Curr Biol. 2009 Dec 29;19(24):2102-7. doi: 10.1016/j.cub.2009.10.075. Curr Biol. 2009. PMID: 20022245
-
How to shape a cylinder: pollen tube as a model system for the generation of complex cellular geometry.Sex Plant Reprod. 2010 Mar;23(1):63-71. doi: 10.1007/s00497-009-0121-4. Epub 2009 Nov 18. Sex Plant Reprod. 2010. PMID: 20165964 Review.
-
The cellular mechanics of an invasive lifestyle.J Exp Bot. 2013 Nov;64(15):4709-28. doi: 10.1093/jxb/ert254. Epub 2013 Sep 7. J Exp Bot. 2013. PMID: 24014865 Review.
Cited by
-
External application of gametophyte-specific ZmPMEI1 induces pollen tube burst in maize.Plant Reprod. 2013 Sep;26(3):255-66. doi: 10.1007/s00497-013-0221-z. Epub 2013 Jul 4. Plant Reprod. 2013. PMID: 23824238
-
Quantitative cell biology of tip growth in moss.Plant Mol Biol. 2021 Nov;107(4-5):227-244. doi: 10.1007/s11103-021-01147-7. Epub 2021 Apr 6. Plant Mol Biol. 2021. PMID: 33825083 Free PMC article. Review.
-
Periodic traction in migrating large amoeba of Physarum polycephalum.J R Soc Interface. 2015 May 6;12(106):20150099. doi: 10.1098/rsif.2015.0099. J R Soc Interface. 2015. PMID: 25808339 Free PMC article.
-
Emerging roles for microtubules in angiosperm pollen tube growth highlight new research cues.Front Plant Sci. 2015 Feb 10;6:51. doi: 10.3389/fpls.2015.00051. eCollection 2015. Front Plant Sci. 2015. PMID: 25713579 Free PMC article.
-
Computer models of cell polarity establishment in plants.Plant Physiol. 2023 Aug 31;193(1):42-53. doi: 10.1093/plphys/kiad264. Plant Physiol. 2023. PMID: 37144853 Free PMC article. Review.
References
-
- Aouar L., Chebli Y., Geitmann A. (2010). Morphogenesis of complex plant cell shapes - The mechanical role of crystalline cellulose in growing pollen tubes. Sex. Plant Reprod. 23: 15–27 - PubMed
-
- Bartnicki-Garcia S. (2002). Hyphal tip growth: Outstanding questions. Molecular Biology of Fungal Development, Osiewacz H.D., ed (New York: Marcel Dekker; ), pp. 29–58
-
- Baskin T. (2005). Anisotropic expansion of the plant cell wall. Annu. Rev. Cell Dev. Biol. 21: 203–222 - PubMed
-
- Benkert R., Obermeyer G., Bentrup F.W. (1997). The turgor pressure of growing lily pollen tubes. Protoplasma 198: 1–8
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

