Evolution of gene regulatory networks by fluctuating selection and intrinsic constraints
- PMID: 20700492
- PMCID: PMC2916849
- DOI: 10.1371/journal.pcbi.1000873
Evolution of gene regulatory networks by fluctuating selection and intrinsic constraints
Abstract
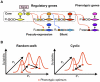
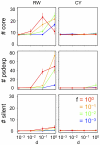
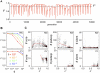
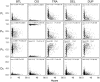
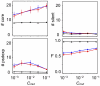
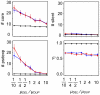
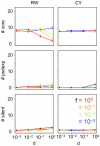
Various characteristics of complex gene regulatory networks (GRNs) have been discovered during the last decade, e.g., redundancy, exponential indegree distributions, scale-free outdegree distributions, mutational robustness, and evolvability. Although progress has been made in this field, it is not well understood whether these characteristics are the direct products of selection or those of other evolutionary forces such as mutational biases and biophysical constraints. To elucidate the causal factors that promoted the evolution of complex GRNs, we examined the effect of fluctuating environmental selection and some intrinsic constraining factors on GRN evolution by using an individual-based model. We found that the evolution of complex GRNs is remarkably promoted by fixation of beneficial gene duplications under unpredictably fluctuating environmental conditions and that some internal factors inherent in organisms, such as mutational bias, gene expression costs, and constraints on expression dynamics, are also important for the evolution of GRNs. The results indicate that various biological properties observed in GRNs could evolve as a result of not only adaptation to unpredictable environmental changes but also non-adaptive processes owing to the properties of the organisms themselves. Our study emphasizes that evolutionary models considering such intrinsic constraining factors should be used as null models to analyze the effect of selection on GRN evolution.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

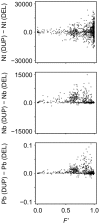
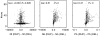
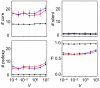
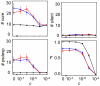


Similar articles
-
Phenotype selection due to mutational robustness.PLoS One. 2024 Nov 18;19(11):e0311058. doi: 10.1371/journal.pone.0311058. eCollection 2024. PLoS One. 2024. PMID: 39556585 Free PMC article.
-
Stochasticity versus determinism: consequences for realistic gene regulatory network modelling and evolution.J Mol Evol. 2010 Feb;70(2):215-31. doi: 10.1007/s00239-010-9323-5. Epub 2010 Feb 12. J Mol Evol. 2010. PMID: 20151115
-
The ensemble of gene regulatory networks at mutation-selection balance.J R Soc Interface. 2023 Jan;20(198):20220075. doi: 10.1098/rsif.2022.0075. Epub 2023 Jan 4. J R Soc Interface. 2023. PMID: 36596452 Free PMC article.
-
Natural selection on crosstalk between gene regulatory networks facilitates bacterial adaptation to novel environments.Curr Opin Microbiol. 2022 Jun;67:102140. doi: 10.1016/j.mib.2022.02.002. Epub 2022 Mar 3. Curr Opin Microbiol. 2022. PMID: 35248980 Review.
-
Using evolutionary computations to understand the design and evolution of gene and cell regulatory networks.Methods. 2013 Jul 15;62(1):39-55. doi: 10.1016/j.ymeth.2013.05.013. Epub 2013 May 30. Methods. 2013. PMID: 23726941 Free PMC article. Review.
Cited by
-
Bistability in feedback circuits as a byproduct of evolution of evolvability.Mol Syst Biol. 2012 Jan 17;8:564. doi: 10.1038/msb.2011.98. Mol Syst Biol. 2012. PMID: 22252387 Free PMC article.
-
Genetic and environmental factors affecting cryptic variations in gene regulatory networks.BMC Evol Biol. 2013 Apr 26;13:91. doi: 10.1186/1471-2148-13-91. BMC Evol Biol. 2013. PMID: 23622056 Free PMC article.
-
ncDNA and drift drive binding site accumulation.BMC Evol Biol. 2012 Aug 30;12:159. doi: 10.1186/1471-2148-12-159. BMC Evol Biol. 2012. PMID: 22935101 Free PMC article.
-
Early effects of gene duplication on the robustness and phenotypic variability of gene regulatory networks.BMC Bioinformatics. 2022 Nov 28;23(1):509. doi: 10.1186/s12859-022-05067-1. BMC Bioinformatics. 2022. PMID: 36443677 Free PMC article.
-
Co-expression network analysis of environmental canalization in the ascidian Ciona.BMC Ecol Evol. 2022 Apr 28;22(1):53. doi: 10.1186/s12862-022-02006-9. BMC Ecol Evol. 2022. PMID: 35484499 Free PMC article.
References
-
- Carroll SB. Evo-devo and an expanding evolutionary synthesis: a genetic theory of morphological evolution. Cell. 2008;134:25–36. - PubMed
-
- Fox CW, Wolf JB. Evolutionary genetics : concepts and case studies. New York: Oxford University Press; 2006.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

