Simulation methods with extended stability for stiff biochemical Kinetics

Abstract

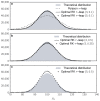
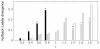
Background: With increasing computer power, simulating the dynamics of complex systems in chemistry and biology is becoming increasingly routine. The modelling of individual reactions in (bio)chemical systems involves a large number of random events that can be simulated by the stochastic simulation algorithm (SSA). The key quantity is the step size, or waiting time, tau, whose value inversely depends on the size of the propensities of the different channel reactions and which needs to be re-evaluated after every firing event. Such a discrete event simulation may be extremely expensive, in particular for stiff systems where tau can be very short due to the fast kinetics of some of the channel reactions. Several alternative methods have been put forward to increase the integration step size. The so-called tau-leap approach takes a larger step size by allowing all the reactions to fire, from a Poisson or Binomial distribution, within that step. Although the expected value for the different species in the reactive system is maintained with respect to more precise methods, the variance at steady state can suffer from large errors as tau grows.

Results: In this paper we extend Poisson tau-leap methods to a general class of Runge-Kutta (RK) tau-leap methods. We show that with the proper selection of the coefficients, the variance of the extended tau-leap can be well-behaved, leading to significantly larger step sizes.

Conclusions: The benefit of adapting the extended method to the use of RK frameworks is clear in terms of speed of calculation, as the number of evaluations of the Poisson distribution is still one set per time step, as in the original tau-leap method. The approach paves the way to explore new multiscale methods to simulate (bio)chemical systems.

Figure 1

Stability and relative variance for the different methods. Stability and relative variance functions for the Poisson τ-leap method (solid line) and RK τ-leap methods with optimal stability regions and bounded relative variance (ψ) with 3 stages (dotted line) and 5 stages (dashed line). Regions fulfilling the bounds on ψ are shown in grey. Square dots correspond to relative variances computed from 10⁶ simulations each. (a), (b): Relative variance bounded by 0.1. (c), (d): Relative variance bounded by 0.25. (e), (f): Relative variance bounded by 0.5.

Figure 2

Histogram of X₁ in the Reversible isomerisation reaction. Histogram of X₁ in the Reversible isomerisation reaction (10⁶ samples used) solved by the SSA (grey background), Poisson τ-leap (dashed line), and optimal RK τ-leap methods with bounded relative variance. (a) τ = 0.05 (z = -1), Optimal RK τ-leap s = 3, ϵ = 0.1 (solid line) and s = 5, ϵ = 0.1 ("+" marks), (b) τ = 0.4 (z = -8), Optimal RK τ-leap s = 3, ϵ = 0.5 (solid line) and s = 5, ϵ = 0.1 ("+" marks), Poisson τ-leap is unstable for this time step. (c) τ = 0.6 (z = -12), Optimal RK τ-leap s = 5, ϵ = 0.5 ("+" marks), Poisson τ-leap and Optimal RK τ-leap s = 3 are unstable for this time step.

Figure 3

Histogram of X in the Schlögl reaction. Histogram of X in the Schlögl reaction (10⁶ samples used) solved by the SSA (grey background), Poisson τ-leap (dashed line), and Optimal RK τ-leap methods. (a) τ = 0.4, Optimal RK τ-leap s = 3, ϵ = 0.1 (solid line) and s = 5, ϵ = 0.1 ("+" marks), (b) τ = 0.8, Optimal RK τ-leap s = 3, ϵ = 0.5 (solid line) and s = 5, ϵ = 0.5 ("+" marks).

Figure 4

Kullback-Leibler divergence for the Schlögl reaction. Kullback-Leibler divergence between the exact stationary distribution of X in the Schlögl reaction (estimated by 10⁶ samples solved by SSA) and the approximate stationary distributions obtained with the Poisson τ-leap (black), Optimal RK s = 3; ϵ = 0.5 (grey lines) and Optimal RK s = 5, ϵ = 0.5 (white). Bars are shown only for the stable method and τ settings. Asterisks denote methods that have a rate of failure above 10^-3.