Motor synergies and the equilibrium-point hypothesis
- PMID: 20702893
- PMCID: PMC2921643
- DOI: 10.1123/mcj.14.3.294
Motor synergies and the equilibrium-point hypothesis
Abstract
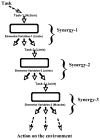
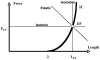
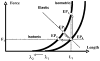
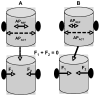
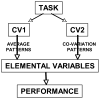
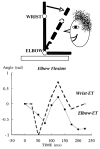
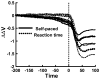
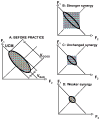
The article offers a way to unite three recent developments in the field of motor control and coordination: (1) The notion of synergies is introduced based on the principle of motor abundance; (2) The uncontrolled manifold hypothesis is described as offering a computational framework to identify and quantify synergies; and (3) The equilibrium-point hypothesis is described for a single muscle, single joint, and multijoint systems. Merging these concepts into a single coherent scheme requires focusing on control variables rather than performance variables. The principle of minimal final action is formulated as the guiding principle within the referent configuration hypothesis. Motor actions are associated with setting two types of variables by a controller, those that ultimately define average performance patterns and those that define associated synergies. Predictions of the suggested scheme are reviewed, such as the phenomenon of anticipatory synergy adjustments, quick actions without changes in synergies, atypical synergies, and changes in synergies with practice. A few models are briefly reviewed.
Figures
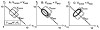
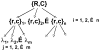
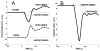
Similar articles
-
Motor control theories and their applications.Medicina (Kaunas). 2010;46(6):382-92. Medicina (Kaunas). 2010. PMID: 20944446 Free PMC article. Review.
-
Postural synergies and their development.Neural Plast. 2005;12(2-3):119-30; discussion 263-72. doi: 10.1155/NP.2005.119. Neural Plast. 2005. PMID: 16097480 Free PMC article. Review.
-
Multi-finger synergies and the muscular apparatus of the hand.Exp Brain Res. 2018 May;236(5):1383-1393. doi: 10.1007/s00221-018-5231-5. Epub 2018 Mar 12. Exp Brain Res. 2018. PMID: 29532100 Free PMC article.
-
Stages in learning motor synergies: a view based on the equilibrium-point hypothesis.Hum Mov Sci. 2010 Oct;29(5):642-54. doi: 10.1016/j.humov.2009.11.002. Epub 2010 Jan 8. Hum Mov Sci. 2010. PMID: 20060610 Free PMC article. Review.
-
Learning effects on muscle modes and multi-mode postural synergies.Exp Brain Res. 2008 Jan;184(3):323-38. doi: 10.1007/s00221-007-1101-2. Epub 2007 Aug 28. Exp Brain Res. 2008. PMID: 17724582 Free PMC article.
Cited by
-
Intentional and unintentional multi-joint movements: their nature and structure of variance.Neuroscience. 2015 Mar 19;289:181-93. doi: 10.1016/j.neuroscience.2014.12.079. Epub 2015 Jan 14. Neuroscience. 2015. PMID: 25596318 Free PMC article.
-
Age-related deficits in bilateral motor synergies and force coordination.BMC Geriatr. 2019 Oct 24;19(1):287. doi: 10.1186/s12877-019-1285-x. BMC Geriatr. 2019. PMID: 31651243 Free PMC article.
-
Assisting Forearm Function in Children With Movement Disorders via A Soft Wearable Robot With Equilibrium-Point Control.Front Robot AI. 2022 Jun 15;9:877041. doi: 10.3389/frobt.2022.877041. eCollection 2022. Front Robot AI. 2022. PMID: 35783026 Free PMC article.
-
Task-specific stability in muscle activation space during unintentional movements.Exp Brain Res. 2014 Nov;232(11):3645-58. doi: 10.1007/s00221-014-4048-0. Epub 2014 Aug 6. Exp Brain Res. 2014. PMID: 25092272 Free PMC article.
-
Synergies in the space of control variables within the equilibrium-point hypothesis.Neuroscience. 2016 Feb 19;315:150-61. doi: 10.1016/j.neuroscience.2015.12.012. Epub 2015 Dec 14. Neuroscience. 2016. PMID: 26701299 Free PMC article.
References
-
- Arimoto S, Tahara K, Yamaguchi M, Nguyen PTA, Han HY. Principles of superposition for controlling pinch motions by means of robot fingers with soft tips. Robotica. 2001;19:21–28.
-
- Aruin AS, Latash ML. Directional specificity of postural muscles in feed-forward postural reactions during fast voluntary arm movements. Experimental Brain Research. 1995;103:323–332. - PubMed
-
- Belen’kii VY, Gurfinkel VS, Pal’tsev YI. Elements of control of voluntary movements. Biofizika. 1967;10:135–141. - PubMed
-
- Bernstein NA. A new method of mirror cyclographie and its application towards the study of labor movements during work on a workbench. Hygiene, Safety and Pathology of Labor. 1930;# 5# 6:3–9. 3–11. in Russian.
-
- Bernstein NA. The problem of interrelation between coordination and localization. Archives of Biological Science. 1935;38:1–35. in Russian.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

