Harmonic pitch: dependence on resolved partials, spectral edges, and combination tones

Abstract

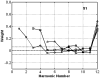
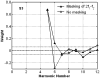
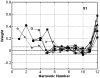
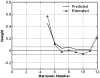
Perceptual weights were estimated in a pitch-comparison experiment to assess the relative influences of individual partial tones on listeners' pitch judgments. The stimuli were harmonic sounds (F0=200 Hz) with partials up to the 12th. Low-numbered partials were removed step-by-step, so that the remaining higher-numbered partials would have a better chance of showing any effect. The individual frequencies of the partials were perturbed randomly on each stimulus presentation, and weights were estimated as the correlation coefficients between the frequency perturbations and the listeners' responses. When the harmonic sounds contained all twelve partials, the listeners depended mostly on the low-numbered, resolved partials within the well-established dominance region. As the low-numbered partials were taken out of the dominance region, the listeners mostly listened to the lowest and highest partials at the spectral edges. For one listener, such an edge-listening strategy took the form of relying on nonlinear combination tones. Overall, there was no indication of any influence on pitch from unresolved partials, thus no evidence of contribution to pitch from temporal cues carried by this group of partials. The estimated patterns of weights were well described by the predictions of Goldstein's optimal-processor model. The predicted weights were inversely proportional to the amount of error for estimating the individual frequencies of the partials. The agreement between the predicted and measured weights suggests that, for harmonic sounds, partials whose frequencies are perceived with the best precision will likely have the greatest influence on perceived pitch.

Figure 1

Stimuli (top) and procedure (bottom) used in the pitch-comparison experiment. The stimuli were harmonic sounds with F0 = 200 Hz and varying number of partials in four conditions. The procedure was two-interval, forced-choice, with the listener indicating which interval had higher pitch.

Figure 2

Weights as a function of harmonic number, from three individual listeners (panels 1 to 3) and their mean (panel 4), and from four conditions (as indicated by different symbols). The two horizontal dotted lines sandwiching the line of zero weight represent plus and minus two standard errors ( $2{\sigma }_e=2/\sqrt{900}$) from zero correlation. In the panels for individual listeners, data points inside the area bounded by these two lines are deemed no different from zero. The error bars in the mean panel show plus and minus one standard error of the mean. The large sizes of the error bars reflect the considerable individual differences in listening strategy.

Figure 2

Weights as a function of harmonic number, from three individual listeners (panels 1 to 3) and their mean (panel 4), and from four conditions (as indicated by different symbols). The two horizontal dotted lines sandwiching the line of zero weight represent plus and minus two standard errors ( $2{\sigma }_e=2/\sqrt{900}$) from zero correlation. In the panels for individual listeners, data points inside the area bounded by these two lines are deemed no different from zero. The error bars in the mean panel show plus and minus one standard error of the mean. The large sizes of the error bars reflect the considerable individual differences in listening strategy.

Figure 2

Weights as a function of harmonic number, from three individual listeners (panels 1 to 3) and their mean (panel 4), and from four conditions (as indicated by different symbols). The two horizontal dotted lines sandwiching the line of zero weight represent plus and minus two standard errors ( $2{\sigma }_e=2/\sqrt{900}$) from zero correlation. In the panels for individual listeners, data points inside the area bounded by these two lines are deemed no different from zero. The error bars in the mean panel show plus and minus one standard error of the mean. The large sizes of the error bars reflect the considerable individual differences in listening strategy.

Figure 2

Weights as a function of harmonic number, from three individual listeners (panels 1 to 3) and their mean (panel 4), and from four conditions (as indicated by different symbols). The two horizontal dotted lines sandwiching the line of zero weight represent plus and minus two standard errors ( $2{\sigma }_e=2/\sqrt{900}$) from zero correlation. In the panels for individual listeners, data points inside the area bounded by these two lines are deemed no different from zero. The error bars in the mean panel show plus and minus one standard error of the mean. The large sizes of the error bars reflect the considerable individual differences in listening strategy.

Figure 3

Weights estimated from S3 in Condition 3, with (filled triangles) or without (unfilled triangles, same as in Fig. 2) a masking noise low-pass filtered at the frequency of the cubic combination tone.

Figure 4

Weights estimated from S1 with spectral shaping applied to the complex sounds. In each condition, the sound pressure level was 40 dB for the lowest partial, 50 dB for the second lowest partial, and 60 dB for all the rest.

Figure 5

Predicted weights (solid line) and the mean estimated weights (circles with dashed line, same as in Fig. 2) for Condition 1. The predictions were derived from Goldstein (1973)’s pitch model.

Figure 6

Predicted weights (solid line) and the mean estimated weights (triangles with dashed line) for Condition 3. Note that the mean results shown here were different from the mean results presented in Fig. 2 for the same condition; they were computed using S3’s weights obtained with the masking noise. Computed this way, the outcome is free from the influence of the combination tone.