A mechanochemical model explains interactions between cortical microtubules in plants

Abstract

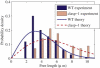
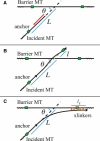
Microtubules anchored to the two-dimensional cortex of plant cells collide through plus-end polymerization. Collisions can result in rapid depolymerization, directional plus-end entrainment, or crossover. These interactions are believed to give rise to cellwide self-organization of plant cortical microtubules arrays, which is required for proper cell wall growth. Although the cell-wide self-organization has been well studied, less emphasis has been placed on explaining the interactions mechanistically from the molecular scale. Here we present a model for microtubule-cortex anchoring and collision-based interactions between microtubules, based on a competition between cross-linker bonding, microtubule bending, and microtubule polymerization. Our model predicts a higher probability of entrainment at smaller collision angles and at longer unanchored lengths of plus-ends. This model addresses observed differences between collision resolutions in various cell types, including Arabidopsis cells and Tobacco cells.

Figure 1

The free lengths L from the MT tip to the last anchoring site. Experimental data from Ambrose and Wasteneys (15). The nonhomogeneous distribution predicted by Eq. 2 provides qualitative agreement for both WT and clasp-1 data.

Figure 2

Three possible collision resolutions. The incident MT collides with a barrier at an angle θ and with free length L. Possible resolutions are (A) catastrophe, in which the incident MT begins shrinking, (B) crossover, in which the incident MT develops a small bend to overpass the barrier and continue growing unperturbed, and (C) plus-end entrainment, in which the incident MT becomes entrained by the barrier via cross-linking proteins (orange online). MTs are shown in black, whereas anchors are shown as green squares.

Figure 3

Collision-induced catastrophe. (A) Two MTs approach a barrier MT. Thermal fluctuations at their tips allows them to either clear the barrier (bottom incident MT), or get temporarily blocked (top incident MT). Anchors are shown as green boxes. (B) Probability of being in the growth stage, i.e., that catastrophe has not yet occurred, versus distance to the barrier MT, for various values of α (log-linear scale). The drop between the prebarrier curve and the postbarrier curves (shown as dashed lines for some α) provides the probability of collision-induced catastrophe.

Figure 4

A mechanical pathway to entrainment. An incident MT encounters a barrier MT at an approach angle θ. The incident MT is slightly bent due to thermal fluctuations and, at the point of intersection, makes an angle θ_X with the barrier MT. (Inset) Cross-linkers (red online) attach two intersecting MTs. The cross-linkers vary in length, l_i ∈ [l₀, l_M] and are spaced δ apart. Distance along the bisector to the i^th cross-linker is x_i.

Figure 5

Collision resolution probabilities. (A) Probability of entrainment given by Eq. 17 for WT (solid) and clasp-1 (dashed) anchoring kinetics. (Dashed lines) Upper bound for probability of collision-induced catastrophe. (B) Distribution of zippering angles for WT and clasp-1 anchoring kinetics, along with experimental histograms from Ambrose and Wasteneys (15). These are calculated from the results in panel A using Bayes' rule. In the experimental histograms, we exclude entrainment events at <20° as low-angle entrainment events are difficult to resolve experimentally.