Coverage statistics for sequence census methods

Abstract

Background: We study the statistical properties of fragment coverage in genome sequencing experiments. In an extension of the classic Lander-Waterman model, we consider the effect of the length distribution of fragments. We also introduce a coding of the shape of the coverage depth function as a tree and explain how this can be used to detect regions with anomalous coverage. This modeling perspective is especially germane to current high-throughput sequencing experiments, where both sample preparation protocols and sequencing technology particulars can affect fragment length distributions.

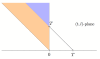
Results: Under the mild assumptions that fragment start sites are Poisson distributed and successive fragment lengths are independent and identically distributed, we observe that, regardless of fragment length distribution, the fragments produced in a sequencing experiment can be viewed as resulting from a two-dimensional spatial Poisson process. We then study the successive jumps of the coverage function, and show that they can be encoded as a random tree that is approximately a Galton-Watson tree with generation-dependent geometric offspring distributions whose parameters can be computed.

Conclusions: We extend standard analyses of shotgun sequencing that focus on coverage statistics at individual sites, and provide a null model for detecting deviations from random coverage in high-throughput sequence census based experiments. Our approach leads to explicit determinations of the null distributions of certain test statistics, while for others it greatly simplifies the approximation of their null distributions by simulation. Our focus on fragments also leads to a new approach to visualizing sequencing data that is of independent interest.

Figure 1

A coverage function, lattice path excursion, and rooted tree. A coverage function is depicted in (A) with its associated lattice path excursion (0,1,2,3,4,3,2,3,4,5,4,3,2,3,2,1,0) in (B). The lattice path excursion in (B) differs from the function (A) in that it records only the jumps of (A). It does not give any information regarding how long the function remains at each y-value. The rooted tree for the coverage function is in (C). The rooted tree is equivalent to the lattice path excursion (B). The red squares in (B) are the equivalence class representatives.

Figure 2

A two dimensional view of a sequencing experiment. A typical wedge in the (t,l) plane is shown. Each interval gives a point (t_i,l_i) in this plane where t_i gives the start position of an interval and l_i gives the length. The number of points in the green wedge gives the height $X_{t_0}$ of the coverage function at t₀.

Figure 3

A wedge from the planar Poisson process. The intervals that correspond to points in both the blue and orange regions contribute to the height X₀. Any point in the orange region would "die" before T while points in the blue region contribute to the height X_T.

Figure 4

Comparison of the Poisson process and Markov approximation in terms of tree height. Histograms of the densities for tree height are shown for trees built from a simulated Poisson process (solid yellow) and Galton-Watson trees from the Markov approximation (blue striped) for the case of fixed fragment lengths. Each tree corresponds to one lattice path excursion away from 0 (also referred to as sequence islands or contigs). The simulations include average height θ = 6 with 14,466 trees simulated for each type (A), θ = 9 with 3,551 trees simulated for each type (B), θ = 12 with 1,429 trees simulated for each type (C), and θ = 15 with 217 trees simulated for each type (D).

Figure 5

Comparison of trees built from the Poisson process with the probability r(1, H). The function r(1,H) = Π{Galton-Watson tree has height ≥ H} is plotted in red. Using trees from a simulated Poisson process, the function Π{tree from simulated Poisson process has height ≥ H} is plotted in blue. The plots include average height θ = 6 (A), θ = 9 (B), θ = 12 (C) and θ = 15 (D) for the case of fixed fragment lengths.

Figure 6

Examples of sequencing in the (t,l) plane. (A) Fragments from a sequencing experiment shown in the (t,l) plane. (B) The spatial Poisson process resulting from fragments with the same length distribution as (A) but with position sampled uniformly at random.