Periodicity and evoked responses in motor cortex
- PMID: 20739573
- PMCID: PMC2952881
- DOI: 10.1523/JNEUROSCI.5947-09.2010
Periodicity and evoked responses in motor cortex
Erratum in
- J Neurosci. 2013 Jan 30;33(5):2237
Abstract
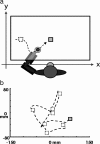
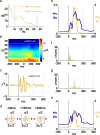
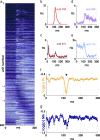
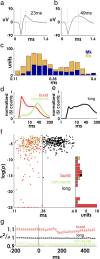
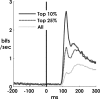
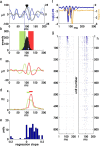
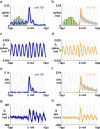
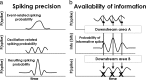
Spiking in primary motor cortex (MI) exhibits a characteristic beta frequency periodicity, but the functional relevance of this rhythmic firing is controversial. We simultaneously recorded multiple single units and local field potentials in MI in two monkeys (Macaca mulatta) during continuous, self-paced movements to serially presented targets. We find that the appearance of each new target evokes precisely timed spiking in MI at a characteristic latency but that the exact timing of this response varies depending on its relationship to the phase of the ongoing beta range oscillation. As a result of this interaction between evoked spiking and endogenous beta periodicity, we find that the amount of information about target location encoded in the spiking of MI neurons is not simply a function of elapsed time but depends also on oscillatory phase. Our results suggest that periodicity may be an important feature of the early stages of sensorimotor processing in the cortical motor system.
Figures
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
