Characterization of Atrophic Changes in the Cerebral Cortex Using Fractal Dimensional Analysis

Abstract

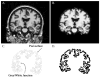
The purpose of this project is to apply a modified fractal analysis technique to high-resolution T1 weighted magnetic resonance images in order to quantify the alterations in the shape of the cerebral cortex that occur in patients with Alzheimer's disease. Images were selected from the Alzheimer's Disease Neuroimaging Initiative database (Control N=15, Mild-Moderate AD N=15). The images were segmented using a semi-automated analysis program. Four coronal and three axial profiles of the cerebral cortical ribbon were created. The fractal dimensions (D(f)) of the cortical ribbons were then computed using a box-counting algorithm. The mean D(f) of the cortical ribbons from AD patients were lower than age-matched controls on six of seven profiles. The fractal measure has regional variability which reflects local differences in brain structure. Fractal dimension is complementary to volumetric measures and may assist in identifying disease state or disease progression.

Fig. 1

Example of two-dimensional cortical ribbons from a control subject and a patient with Alzheimer’s disease taken from seven locations. Cortical ribbons from seven sectioning planes (four coronal and three axial) were selected for fractal analysis. The locations and orientations of these planes are described in the text. The first row identifies these planes as solid white lines on a mid-line saggital image. Non-cortical structures (cerebellum, white matter, deep grey matter, and brain stem) were not included in the fractal analysis of the cerebral cortex, but are displayed for spatial reference purposes. The second row displays the cortical ribbon extracted from a control patient with normal cognition (CDR=0). In the third row, the cortical ribbons from the same locations are shown for a patient with moderate Alzheimer’s disease (CDR=2). Note the thinner cortical ribbon and widened sulci in the patient compared to the control subject was 0.9973 (Model 2, Individual). The ICC for the fractal dimension analysis

Fig. 2

Magnetic resonance image segmentation and cortical ribbon generation. This figure shows some of the key steps involved in generating a two-dimensional projection of the ribbon of cerebral cortex. Please see the text for full details. a This panel shows original magnetic resonance image generated using the MP-RAGE (T1 weighted) sequence. This coronal slice was taken through the mammillary bodies. b This is the image after intensity normalization, skull-stripping, and removal of brain stem. c The grey/white surface is generated using intensity differences between the grey and white matter on the normalized image. The pial surface was generated using outward deformation of the grey/white surface. d The space between the two surfaces in panel C is filled to create the cortical ribbon

Fig. 3

Computing fractal dimension using a box-counting algorithm. a An object is tiled with boxes of a given size, and the number of boxes needed to cover the object is counted. The box size is changed, and the process is repeated. Four examples of tiling are shown in this panel. b The fractal dimension of an object is computed by determining the ratio of the change in box count to the change in box size (in log–log space). The least squares regression for all data points is indicated by the solid line. c To determine the spatial range over which the image shows scale invariance, the change in point-to-point slope is plotted. Those point-pairs with slopes less than the threshold (±0.1) are highlighted in pink. d The data from panel (b) are shown, but the regression line is taken only through the linear portion

Fig. 4

The effects of cortical thickness and gyrification index on measured fractal dimensionality. A coronal slice from a control subject and its fractal dimension is seen in the box. The remaining cortical ribbons are artificial data demonstrating fractal dimension changes with variation in cortical thickness, gyrification index, and the combination of the two. The fractal dimension of each slice is indicated by the number below the slice. Changes in cortical thickness are seen on the horizontal axis with increasing thickness towards the right. Changes in the gyrification index are seen on the vertical axis with values increasing upwards. Thinning of the cortical ribbon and lowering the gyrification index both decrease fractal dimensionality

Fig. 5

Fractal dimension scatter-plot for 18 scans of patients in two diagnostic categories. The cortical ribbons for 30 MR scans were analyzed in seven locations described in Fig. 2 using the methods described in Fig. 3 and in the text. For each location, the fractal dimension of the cortical ribbon is plotted for each patient. The solid lines indicate the average scores for each performance category. The dotted lines indicate ± one standard error of the mean. The subjects are grouped according to clinical category with red squares indicating controls (MMSE scores 28–30) and blue triangles indicating the patients (MMSE scores 17–23). The average fractal dimension was higher in all locations for the control group compared to the patient group. The values were statistically significant for all four coronal locations as well as the first two axial locations. See Table 2 for details on the statistical analysis