Mathematical description of bacterial traveling pulses
- PMID: 20808878
- PMCID: PMC2924242
- DOI: 10.1371/journal.pcbi.1000890
Mathematical description of bacterial traveling pulses
Abstract
The Keller-Segel system has been widely proposed as a model for bacterial waves driven by chemotactic processes. Current experiments on Escherichia coli have shown the precise structure of traveling pulses. We present here an alternative mathematical description of traveling pulses at the macroscopic scale. This modeling task is complemented with numerical simulations in accordance with the experimental observations. Our model is derived from an accurate kinetic description of the mesoscopic run-and-tumble process performed by bacteria. This can account for recent experimental observations with E. coli. Qualitative agreements include the asymmetry of the pulse and transition in the collective behaviour (clustered motion versus dispersion). In addition, we can capture quantitatively the traveling speed of the pulse as well as its characteristic length. This work opens several experimental and theoretical perspectives since coefficients at the macroscopic level are derived from considerations at the cellular scale. For instance, the particular response of a single cell to chemical cues turns out to have a strong effect on collective motion. Furthermore, the bottom-up scaling allows us to perform preliminary mathematical analysis and write efficient numerical schemes. This model is intended as a predictive tool for the investigation of bacterial collective motion.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
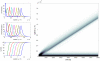
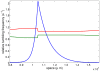
Similar articles
-
Traveling Pulses for a Two-Species Chemotaxis Model.PLoS Comput Biol. 2016 Apr 12;12(4):e1004843. doi: 10.1371/journal.pcbi.1004843. eCollection 2016 Apr. PLoS Comput Biol. 2016. PMID: 27071058 Free PMC article.
-
Macroscopic equations for bacterial chemotaxis: integration of detailed biochemistry of cell signaling.J Math Biol. 2015 Jan;70(1-2):1-44. doi: 10.1007/s00285-013-0748-5. Epub 2013 Dec 24. J Math Biol. 2015. PMID: 24366373
-
Spatio-temporal structure of migrating chemotactic band of Escherichia coli. I. Traveling band profile.Biophys J. 1979 May;26(2):243-61. doi: 10.1016/S0006-3495(79)85248-0. Biophys J. 1979. PMID: 400469 Free PMC article.
-
Overview of mathematical approaches used to model bacterial chemotaxis II: bacterial populations.Bull Math Biol. 2008 Aug;70(6):1570-607. doi: 10.1007/s11538-008-9322-5. Epub 2008 Jul 19. Bull Math Biol. 2008. PMID: 18642047 Review.
-
Overview of mathematical approaches used to model bacterial chemotaxis I: the single cell.Bull Math Biol. 2008 Aug;70(6):1525-69. doi: 10.1007/s11538-008-9321-6. Epub 2008 Jul 19. Bull Math Biol. 2008. PMID: 18642048 Review.
Cited by
-
Microfluidics expanding the frontiers of microbial ecology.Annu Rev Biophys. 2014;43:65-91. doi: 10.1146/annurev-biophys-051013-022916. Annu Rev Biophys. 2014. PMID: 24773019 Free PMC article. Review.
-
Traveling Pulses for a Two-Species Chemotaxis Model.PLoS Comput Biol. 2016 Apr 12;12(4):e1004843. doi: 10.1371/journal.pcbi.1004843. eCollection 2016 Apr. PLoS Comput Biol. 2016. PMID: 27071058 Free PMC article.
-
Connecting single-cell properties to collective behavior in multiple wild isolates of the Enterobacter cloacae complex.PLoS One. 2019 Apr 4;14(4):e0214719. doi: 10.1371/journal.pone.0214719. eCollection 2019. PLoS One. 2019. PMID: 30947254 Free PMC article.
-
Bacterial bioconvection confers context-dependent growth benefits and is robust under varying metabolic and genetic conditions.J Bacteriol. 2023 Oct 26;205(10):e0023223. doi: 10.1128/jb.00232-23. Epub 2023 Oct 3. J Bacteriol. 2023. PMID: 37787517 Free PMC article.
-
Derivation of the bacterial run-and-tumble kinetic equation from a model with biochemical pathway.J Math Biol. 2016 Nov;73(5):1161-1178. doi: 10.1007/s00285-016-0985-5. Epub 2016 Mar 18. J Math Biol. 2016. PMID: 26993136
References
-
- Adler J. Chemotaxis in bacteria. Science. 1966;153:708–716. - PubMed
-
- Budrene E, Berg H. Dynamics of formation of symmetrical patterns by chemotactic bacteria. Nature. 1995;376:49–53. - PubMed
-
- Berg H. E. coli in motion. Springer; 2004.
-
- Alt W. Biased random walk models for chemotaxis and related diffusion approximations. J Math Biol. 1980;9:147–177. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

