A new measure of centrality for brain networks
- PMID: 20808943
- PMCID: PMC2922375
- DOI: 10.1371/journal.pone.0012200
A new measure of centrality for brain networks
Abstract
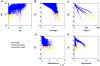
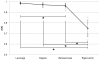
Recent developments in network theory have allowed for the study of the structure and function of the human brain in terms of a network of interconnected components. Among the many nodes that form a network, some play a crucial role and are said to be central within the network structure. Central nodes may be identified via centrality metrics, with degree, betweenness, and eigenvector centrality being three of the most popular measures. Degree identifies the most connected nodes, whereas betweenness centrality identifies those located on the most traveled paths. Eigenvector centrality considers nodes connected to other high degree nodes as highly central. In the work presented here, we propose a new centrality metric called leverage centrality that considers the extent of connectivity of a node relative to the connectivity of its neighbors. The leverage centrality of a node in a network is determined by the extent to which its immediate neighbors rely on that node for information. Although similar in concept, there are essential differences between eigenvector and leverage centrality that are discussed in this manuscript. Degree, betweenness, eigenvector, and leverage centrality were compared using functional brain networks generated from healthy volunteers. Functional cartography was also used to identify neighborhood hubs (nodes with high degree within a network neighborhood). Provincial hubs provide structure within the local community, and connector hubs mediate connections between multiple communities. Leverage proved to yield information that was not captured by degree, betweenness, or eigenvector centrality and was more accurate at identifying neighborhood hubs. We propose that this metric may be able to identify critical nodes that are highly influential within the network.
Conflict of interest statement
Figures


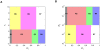
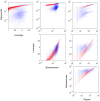

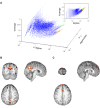
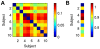



References
-
- Eguiluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV. Scale-free brain functional networks. Physical Review Letters. 2005;94:018102. - PubMed
-
- van den Heuvel MP, Stam CJ, Boersma M, Pol HEH. Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain. Neuroimage. 2008;43:528–539. - PubMed
-
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nature Review neuroscience. 2009;10:186–198. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

