Learning priors for Bayesian computations in the nervous system
- PMID: 20844766
- PMCID: PMC2937037
- DOI: 10.1371/journal.pone.0012686
Learning priors for Bayesian computations in the nervous system
Abstract
Our nervous system continuously combines new information from our senses with information it has acquired throughout life. Numerous studies have found that human subjects manage this by integrating their observations with their previous experience (priors) in a way that is close to the statistical optimum. However, little is known about the way the nervous system acquires or learns priors. Here we present results from experiments where the underlying distribution of target locations in an estimation task was switched, manipulating the prior subjects should use. Our experimental design allowed us to measure a subject's evolving prior while they learned. We confirm that through extensive practice subjects learn the correct prior for the task. We found that subjects can rapidly learn the mean of a new prior while the variance is learned more slowly and with a variable learning rate. In addition, we found that a Bayesian inference model could predict the time course of the observed learning while offering an intuitive explanation for the findings. The evidence suggests the nervous system continuously updates its priors to enable efficient behavior.
Conflict of interest statement
Figures

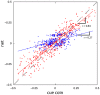
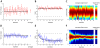
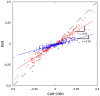


References
-
- Weiss Y, Simoncelli EP, Adelson EH. Motion illusions as optimal percepts. Nat Neurosci. 2002;5:598–604. - PubMed
-
- Stocker AA, Simoncelli EP. Noise characteristics and prior expectations in human visual speed perception. Nat Neurosci. 2006;9:578–585. - PubMed
-
- Jacobs RA. Optimal integration of texture and motion cues to depth. Vision Res. 1999;39:3621–3629. - PubMed
-
- Kording KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427:244–247. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

