Synapses with short-term plasticity are optimal estimators of presynaptic membrane potentials

Abstract

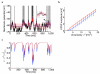
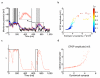
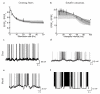
The trajectory of the somatic membrane potential of a cortical neuron exactly reflects the computations performed on its afferent inputs. However, the spikes of such a neuron are a very low-dimensional and discrete projection of this continually evolving signal. We explored the possibility that the neuron's efferent synapses perform the critical computational step of estimating the membrane potential trajectory from the spikes. We found that short-term changes in synaptic efficacy can be interpreted as implementing an optimal estimator of this trajectory. Short-term depression arose when presynaptic spiking was sufficiently intense as to reduce the uncertainty associated with the estimate; short-term facilitation reflected structural features of the statistics of the presynaptic neuron such as up and down states. Our analysis provides a unifying account of a powerful, but puzzling, form of plasticity.

Figure 1

Estimating the presynaptic membrane potential from spiking information. (a) Sample trace (black) of the presynaptic membrane potential generated by an Ornstein-Uhlenbeck process. When the membrane potential exceeds a soft threshold, action potentials (vertical black lines) are generated. The optimal estimator of the presynaptic membrane potential (red line, mean estimate ${\widehat{u}}_t$; red shading, one s.d. σ_t) closely matches an optimally tuned canonical model of short-term plasticity (blue). Inset shows a magnified section. (b) EPSP amplitude of the optimal estimator (red, mean ± s.d.) and of the canonical model of short-term plasticity (blue, mean ± s.d.) as a function of the estimator uncertainty σ². Note that EPSP amplitudes in the biophysical model tend to be smaller than those in the optimal estimator, which is compensating for a somewhat slower decay in the biophysical model (see inset in a). (c) The dynamics of the scaled uncertainty ${\sigma }^2∕{\sigma }_{\max }^2$ (red) closely match the resource variable x_t of the canonical model of STP (blue), σ².

Figure 2

Estimating the presynaptic membrane potential when the resting membrane potential randomly switches between two different values. (a) Presynaptic subthreshold membrane potential with action potentials (black), its optimal mean estimate ($\widehat{u}$, red line) with the associated s.d. (σ, red shading), and the postsynaptic membrane potential in a model synapse with optimally tuned short-term plasticity (blue line). Inset, the (scaled) optimal estimator (red solid line) strongly depends on the estimated probability ρ of being in the up state (red dashed line). (b) EPSP amplitude in the optimal estimator depends on its uncertainty (horizontal axis, σ²) and the change in the estimated probability that the presynaptic cell is in its up state (color code, Δρ). (c) The estimated probability that the presynaptic cell is in its up state ρ (red) tracks the state of the presynaptic neuron (black) as it randomly switches between its up and down states. (d) EPSP magnitudes in the optimal estimator against EPSP magnitudes in the model synapse.

Figure 3

The optimal estimator reproduces experimentally observed patterns of synaptic depression and facilitation. (a) Synaptic depression in cerebellar climbing fibers (circles: mean ± s.e.m.; redrawn from ref. 6) and in the model (solid line), measured as the ratio of the amplitude of the eighth and first EPSP as a function of the stimulation rate during a train of eight presynaptic spikes. (b) Synaptic facilitation in hippocampal Schäffer collaterals (circles, mean ± s.e.m.; redrawn from ref. 39) and in the model (solid line), measured as the ratio of the amplitude of the second and first EPSP as a function of the interval between a pair of presynaptic spikes. Shading in a and b shows the robustness of the fits (Online Methods): model predictions when best-fit parameters are perturbed by 5% (dark gray) or 10% (light gray). (c–d) Predictions of the model for the dynamics of inferior olive neurons (c) and hippocampal pyramidal neurons (d). Sample traces were generated with parameters fitted to the data about STP in cerebellar climbing fibers (shown in a) and Schäffer collaterals (shown in b). (e–f) In vivo intracellular recordings from inferior olive neurons of the (anesthetized) rat (e, reproduced from ref. 40) and hippocampal pyramidal cells of the behaving rat (f, reproduced from ref. 38).

Figure 4

Estimation performance of the presynaptic membrane potential. (a) Performance as a function of the determinism of presynaptic spiking, β (Online Methods), in the optimal estimator (red), an optimally fitted dynamic synapse (blue) and an optimally fitted static synapse without short-term plasticity (green). When β = 0 (entirely stochastic spiking), spikes are generated independently of the membrane potential and, as a consequence, all models fail to track the membrane potential. As β becomes larger (more deterministic spiking), the dynamic synapse model matches the optimal estimator in performance and substantially outperforms the static synapse. Realistic values for βσ_OU (here σ_OU = 1 mV) have been found to be between 2 and 3 in L5 pyramidal cells of somatosensory cortex. (b) Estimation performance with stochastic vesicle release as a function of the number of synaptic release sites, N. The dynamic synapse (blue) tracked the performance of the optimal estimator (red) well and outperformed the static synapse (green) at all values of N. The performance of all estimators decreases only when the number of independent release sites becomes very low (N = 1 or 2 ). When N is large (N → ∞), synaptic transmission becomes deterministic, even though spike generation itself remains stochastic (with parameter β = 2 shown by the arrow in a).