Kinesin recycling in stationary membrane tubes

Abstract

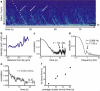
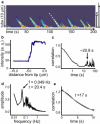
Collections of motors dynamically organize to extract membrane tubes. These tubes grow but often pause or change direction as they traverse an underlying microtubule (MT) network. In vitro, membrane tubes also stall: they stop growing in length despite a large group of motors available at the tip to pull them forward. In these stationary membrane tubes in vitro, we find that clusters of processive kinesin motors form and reach the tip of the tube at regular time intervals. The average times between cluster arrivals depends on the time over which motors depart from the tip, suggesting that motors are recycled toward the tip. Numerical simulations of the motor dynamics in the membrane tube and on the MTs show that the presence of cooperative binding between motors quantitatively accounts for the clustering observed experimentally. Cooperative binding along the length of the MT and a nucleation point at a distance behind the tip define the recycling period. Based on comparison of the numerical results and experimental data, we estimate a cooperative binding probability and concentration regime where the recycling phenomenon occurs.

Figure 1

Kinesin dynamics in membrane tubes. (a) Membrane tubes formed by kinesin motors. The image is a sum of a series of images tracing kinesin-bound fluorescent lipids dynamics in a membrane tube network. The star indicates the point at which the membrane tube is connected to the underlying MT (MTs not visible). Scale bar, 5 μm. (b) Cartoon showing the geometry of a membrane tube of length L extending from a GUV. The tube is anchored to the MT a distance X behind the tip.

Figure 2

Motor cluster timescale. (a) Kymograph tracing the motor dynamics in the direction of the dashed arrow of Fig. 1a in time. The arrows indicate examples of new kinesin motor clusters. The dashed line traces along a growing motor cluster as it moves to the tip. (b) Intensity profile following the dashed line in panel a. Approximately 5 μm behind the tip, motors begin to accumulate and the cluster grows as it reaches the tip of the membrane tube. (c) Autocorrelation curve in time, averaged for all points along the membrane tube of Fig. 1. The correlation curve shows distinct peaks at ≈11 s and 22 s (n = 18). (d) The peak at ∼11 s is confirmed by a peak in the power spectrum (n = 18). (e) The autocorrelation curve at the very tip of the membrane tube (the tip-most 0.33 μm) is fit with an exponential decay. The decay time of this fit represents the time, 12.6 ± 0.5 s, it takes for clusters at the tip to dissipate (n = 3). (f) Plot of the tip decay time versus the typical cluster arrival time for five individual tubes from different experiments. The times at which motor clusters form is linearly related to the release of motors from the tube where t_decay = (0.97 ± 0.05)t_arrival.

Figure 3

Model schematic. Motors bind randomly anywhere along the MT lattice with a probability p_b and a distance X behind the tip of the membrane tube with a probability p_b(X). However, if a diffusing motor neighbors a motor that is already bound to the MT lattice, the diffusing motor will bind next to it on the MT with a probability p_b^∗. Once on the MT lattice, motors may walk toward the tip of the MT or detach from the MT with a probability p_u and at the very tip with a probability p_u^∗.

Figure 4

Simulations. (a) Kymograph from a simulation where motors bind cooperatively and with a nucleation point at X. Here N = 100, L = 10 μm, and X = 5 μm. Motor clusters appear approximately every 20 s. (b) Intensity profile tracing the growing cluster indicated by the dashed line in panel a. Motors begin to accumulate at the nucleation point 5 μm behind the tip. (c) Spatially averaged autocorrelation curve of the signal in panel a showing a distinct peak at ≈20.8 s (n = 15). (d) Spatially averaged power spectrum of the signal with a peak at 20.4 s (n = 15). (e) Autocorrelation curve of the fluorescence signal at the tip of the membrane tube, fit with an exponential decay that gives a cluster dissipation time of 17 s (n = 3).

Figure 5

Average arrival time versus decay time at the tip from simulations. Scatterplot of simulated data for different motor number (N), length (L), and X. The different symbols represent different values of N. For fixed N, moving X to a position farther away from the tip (open symbols represent a larger X) results in an increase in timescales. The experimental data points (triangles) fall into the simulation regime. Error bars for the simulated data points are calculated based on accuracy of the correlation-curve fit as well as the variance between the different simulation values. The individual experimental data points, however, are each from a single membrane tube where the error only represents accuracy of the correlation-curve fit. The error bars are larger in the simulations than in the experimental data because each of the individual simulation points accounts for multiple simulations under the exact same motor number, tube length, and nucleation point conditions. The points with the largest error bars are from simulations where the nucleation point is far behind the tip. A nucleation point that is farther behind the tip takes longer for motors diffusing in the membrane tube to pass by, making the absolute time at which a new motor cluster starts to form more variable resulting in larger error bars.