Origin of twist-bend coupling in actin filaments

Abstract

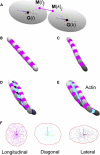
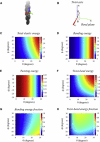
Actin filaments are semiflexible polymers that display large-scale conformational twisting and bending motions. Modulation of filament bending and twisting dynamics has been linked to regulatory actin-binding protein function, filament assembly and fragmentation, and overall cell motility. The relationship between actin filament bending and twisting dynamics has not been evaluated. The numerical and analytical experiments presented here reveal that actin filaments have a strong intrinsic twist-bend coupling that obligates the reciprocal interconversion of bending energy and twisting stress. We developed a mesoscopic model of actin filaments that captures key documented features, including the subunit dimensions, interaction energies, helicity, and geometrical constraints coming from the double-stranded structure. The filament bending and torsional rigidities predicted by the model are comparable to experimental values, demonstrating the capacity of the model to assess the mechanical properties of actin filaments, including the coupling between twisting and bending motions. The predicted actin filament twist-bend coupling is strong, with a persistence length of 0.15-0.4 μm depending on the actin-bound nucleotide. Twist-bend coupling is an emergent property that introduces local asymmetry to actin filaments and contributes to their overall elasticity. Up to 60% of the filament subunit elastic free energy originates from twist-bend coupling, with the largest contributions resulting under relatively small deformations. A comparison of filaments with different architectures indicates that twist-bend coupling in actin filaments originates from their double protofilament and helical structure.

Figure 1

Microscopic organization of model filaments. (A) Schematic of filament subunits modeled as ellipsoids connected by elastic bonds. The subunit centers of mass are given by G(k) or G(l) and their respective bond attachment coordinates by M(k)_j and M(l)_j). (B–E) Schematic of filament resting configurations: single-stranded nonhelical (B), single-stranded helical (C), aligned double-stranded helical (D), and staggered double-stranded helical (E). Longitudinal contacts are colored magenta, diagonal contacts are colored cyan, and lateral contacts are colored dark blue. (F) Schematic of subunit interface bond attachment dispersion areas. The interface is the convex envelope of the bond projections onto the plane normal to the line connecting the center of mass connecting two neighboring subunits.

Figure 2

Equilibrium configurations of resting and strained filaments. Filaments of differing microscopic organization were loaded without twisting along the long filament axis. At equilibrium, configurations result from the balance between load-induced bending, responsible for large in-plane loops, and intrinsic twist-bend coupling arising from the microscopic subunit organization, responsible for out-of plane buckling. (A) Top and side views: single-stranded, nonhelical filaments do not present intrinsic twist-bend coupling. (B) Top and side views: helical filaments show minute out-of-plane buckling, indicating that the helicity present in the resting configuration is sufficient to drive the loop out of the bending plane. The equilibrium configuration for double-stranded with aligned (C) or staggered (D) subunits filaments presents a marked deviation from planar buckling alone, showing the presence of a strong coupling at the microscopic subunit arrangement level.

Figure 3

Bending, twisting, and coupling persistence length landscapes. (A–D) Dependence of the bending, twisting, and coupling persistence lengths of single-stranded nonhelical (A), single-stranded helical (B), aligned double-stranded helical (C), and staggered double-stranded helical (D) filaments on the intersubunit bond stiffness and average subunit interface area. Note that the scales differ among panels and that both helicity and double-stranded structures contribute to the emergence of twist-bend coupling. The star and dot in panel D correspond to the average bond stiffness and interface areas of ATP-actin (14.6 nm², 165 k_BT.nm⁻²) and ADP-actin (14.6 nm², 55 k_BT.nm⁻²) filaments, respectively. The ATP- and ADP-actin filament bond stiffnesses range from 50 to 150 kcal mol⁻¹ nm⁻² and 20 to 50 kcal mol⁻¹ nm⁻², respectively (21). Normalization of the elastic free energy by k_BT yields a corresponding range of 80–250 k_BT nm⁻² for ATP-actin and 30–80 k_BT.nm⁻² for ADP-actin filaments.

Figure 4

Contributions of bending, twisting, and coupling to the total elastic free energy. (A and B) Geometric coordinates associated with orientation of an individual filament subunit (see also Fig. S5) used to quantitate the elastic free-energy terms originating from bending, twisting, and coupling. The vector of strain rotation, κ, is determined by angles θ and ϕ, respectively. The angle between κ and the vertical axis is denoted by θ; the angle between the direction Ox and the projection of κ on the Oxy plane is ϕ. Note that a twist along the long subunit axis, parallel to the filament long axis, corresponds to a vector κ aligned with the vertical axis (i.e., θ = 0 or 180°); conversely, when θ = 90°, the rotation imposed to the subunit corresponds to bending. The angle ϕ controls the degree of coupling between bending and twisting strains. The rotation imposed to the subunit corresponds to an angle of 1 rad about the axis along the unit vector κ. (C–F) The dependence of total (C), bending (D), twisting (E), and coupling (F) elastic free energies on the angular strain rotation. (G and H) The fractional contributions from bending and coupling.