Dimensionality estimation for optimal detection of functional networks in BOLD fMRI data
- PMID: 20858546
- PMCID: PMC3052418
- DOI: 10.1016/j.neuroimage.2010.09.034
Dimensionality estimation for optimal detection of functional networks in BOLD fMRI data
Abstract
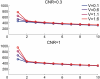
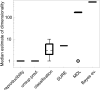
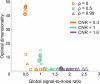
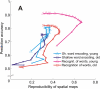
Estimation of the intrinsic dimensionality of fMRI data is an important part of data analysis that helps to separate the signal of interest from noise. We have studied multiple methods of dimensionality estimation proposed in the literature and used these estimates to select a subset of principal components that was subsequently processed by linear discriminant analysis (LDA). Using simulated multivariate Gaussian data, we show that the dimensionality that optimizes signal detection (in terms of the receiver operating characteristic (ROC) metric) goes through a transition from many dimensions to a single dimension as a function of the signal-to-noise ratio. This transition happens when the loci of activation are organized into a spatial network and the variance of the networked, task-related signals is high enough for the signal to be easily detected in the data. We show that reproducibility of activation maps is a metric that captures this switch in intrinsic dimensionality. Except for reproducibility, all of the methods of dimensionality estimation we considered failed to capture this transition: optimization of Bayesian evidence, minimum description length, supervised and unsupervised LDA prediction, and Stein's unbiased risk estimator. This failure results in sub-optimal ROC performance of LDA in the presence of a spatially distributed network, and may have caused LDA to underperform in many of the reported comparisons in the literature. Using real fMRI data sets, including multi-subject group and within-subject longitudinal analysis we demonstrate the existence of these dimensionality transitions in real data.
Copyright © 2010 Elsevier Inc. All rights reserved.
Figures




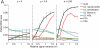
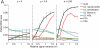




References
-
- Beckmann CF, Smith SM. Probabilistic independent component analysis for functional medical imaging. IEEE Transactions on Medical Imaging. 2004;23(2):137–152. - PubMed
-
- Biehl M, Mietzner A. Statistical mechanics of unsupervised structure recognition. Journal of Physics A. 1994;27:1885–1897.
-
- Bishop CM. Pattern Recognition and Machine Learning. Springer; 2006.
-
- Cordes D, Nandy R. Estimation of intrinsic dimensionality of fMRI data. NeuroImage. 2006;29:145–154. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

