Genomic patterns of pleiotropy and the evolution of complexity
- PMID: 20876104
- PMCID: PMC2964231
- DOI: 10.1073/pnas.1004666107
Genomic patterns of pleiotropy and the evolution of complexity
Abstract
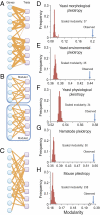
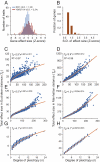
Pleiotropy refers to the phenomenon of a single mutation or gene affecting multiple distinct phenotypic traits and has broad implications in many areas of biology. Due to its central importance, pleiotropy has also been extensively modeled, albeit with virtually no empirical basis. Analyzing phenotypes of large numbers of yeast, nematode, and mouse mutants, we here describe the genomic patterns of pleiotropy. We show that the fraction of traits altered appreciably by the deletion of a gene is minute for most genes and the gene-trait relationship is highly modular. The standardized size of the phenotypic effect of a gene on a trait is approximately normally distributed with variable SDs for different genes, which gives rise to the surprising observation of a larger per-trait effect for genes affecting more traits. This scaling property counteracts the pleiotropy-associated reduction in adaptation rate (i.e., the "cost of complexity") in a nonlinear fashion, resulting in the highest adaptation rate for organisms of intermediate complexity rather than low complexity. Intriguingly, the observed scaling exponent falls in a narrow range that maximizes the optimal complexity. Together, the genome-wide observations of overall low pleiotropy, high modularity, and larger per-trait effects from genes of higher pleiotropy necessitate major revisions of theoretical models of pleiotropy and suggest that pleiotropy has not only allowed but also promoted the evolution of complexity.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
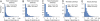

References
-
- Wright S. Evolution and the Genetics of Populations. Chicago: Univ of Chicago Press; 1968.
-
- Hodgkin J. Seven types of pleiotropy. Int J Dev Biol. 1998;42:501–505. - PubMed
-
- Carroll SB. Evo-devo and an expanding evolutionary synthesis: A genetic theory of morphological evolution. Cell. 2008;134:25–36. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

