Fundamental limit of nanophotonic light trapping in solar cells

Abstract

Establishing the fundamental limit of nanophotonic light-trapping schemes is of paramount importance and is becoming increasingly urgent for current solar cell research. The standard theory of light trapping demonstrated that absorption enhancement in a medium cannot exceed a factor of 4n(2)/sin(2)θ, where n is the refractive index of the active layer, and θ is the angle of the emission cone in the medium surrounding the cell. This theory, however, is not applicable in the nanophotonic regime. Here we develop a statistical temporal coupled-mode theory of light trapping based on a rigorous electromagnetic approach. Our theory reveals that the conventional limit can be substantially surpassed when optical modes exhibit deep-subwavelength-scale field confinement, opening new avenues for highly efficient next-generation solar cells.

Fig. 1.

Light trapping with random texture and a grating structure. (A) Light trapping by randomly textured surface. (B) Light trapping using a periodic grating on a back-reflector (yellow); d = 2 μm, L = 250 nm. The depth and width of the dielectric groove in the grating are 50 and 175 nm, respectively. The dielectric material is crystalline silicon. (C) Absorption spectrum [transverse magnetic (TM) mode, normal incidence] and dispersion relation of waveguide modes for the structure in B. The dispersion relation is approximated as , or equivalently in terms of free-space wavelength , where m = 1, 2, 3, … is the band index indicating the field variation in the transverse direction. Resonances occur when k_// = 2π/L (red dots).

Fig. 2.

Light trapping in periodic structures. (A) Blue dots represent channels in the k space. Channels in the circle correspond to free-space propagating modes. (B) Theoretical upper limit of the absorption enhancement factor using a light-trapping scheme where a square-lattice periodic grating structure is introduced into a thin film. Red area represents a spectral range where the upper limit of the absorption enhancement factor F is above 4n².

Fig. 3.

Structure for overcoming the conventional light-trapping limit. (A) A nanophotonic light-trapping structure. The scattering layer consists of a square lattice of air groove patterns with periodicity L = 1200 nm. The thicknesses of the scattering, cladding, and active layers are 80, 60, and 5 nm, respectively. The mirror layer is a perfect electric conductor. (B) The profile of electric-field intensity for the fundamental waveguide mode. Fields are strongly confined in the active layer. To obtain the waveguide mode profile, the scattering layer is modeled by a uniform slab with an averaged dielectric constant.

Fig. 4.

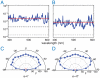
Absorption with the light-trapping structures. (A) Absorption spectrum for normally incident light for the structure shown in Fig. 3. The spectrally averaged absorption (red solid line) is much higher than both the single-pass absorption (light-gray dashed line) and the absorption as predicted by the limit of (dark-gray dashed line). The vertical axis is the absorption coefficient. (B) Absorption spectrum without nanoscale light confinement. The structure is the same as that of A except that the dielectric constant of the active layer is now the same as the cladding layer. The dark-gray dashed line represents the absorption as predicted by the limit of . (C and D) Angular dependence of the spectrally averaged absorption enhancement factor for the structure in Fig. 3. Incident angles are labeled on top of the semicircles. Incident planes are oriented at 0 (C) and 45 (D) degrees (azimuthal angles) with respect to the [10] direction of the lattice. The red circles represent the limit.

Fig. 5.

Illustration of a small active region embedded in a bulk host material: (A) a thin layer, and (B) a spherical inclusion.