Cortical sulcal atlas construction using a diffeomorphic mapping approach

Abstract

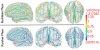
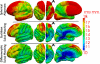
We present a geometric approach for constructing shape atlases of sulcal curves on the human cortex. Sulci and gyri are represented as continuous open curves in R3, and their shapes are studied as elements of an infinite-dimensional sphere. This shape manifold has some nice properties--it is equipped with a Riemannian L2 metric on the tangent space and facilitates computational analyses and correspondences between sulcal shapes. Sulcal mapping is achieved by computing geodesics in the quotient space of shapes modulo rigid rotations and reparameterizations. The resulting sulcal shape atlas is shown to preserve important local geometry inherently present in the sample population. This is demonstrated in our experimental results for deep brain sulci, where we integrate the elastic shape model into surface registration framework for a population of 69 healthy young adult subjects.

Fig. 1

Lateral, frontal, and medial views of, top row: 27 landmark sulci and gyri for 69 subjects, middle row: Euclidean sulcal shape averages, bottom row: Karcher shape average for each landmark type

Fig. 2

Comparison of the geodesic variance for the entire sulcal population for each of the 27 landmarks, both for Euclidean shape averages, as well as elastic shape averages, along the length of the curves

Fig. 3

Lateral, axial, ventral, and medial views of the reconstructed cortical surface with Euclidean sulcal matching (top), and diffeomorphic sulcal matching (bottom). The surfaces are colored according to shape curvedness.

Fig. 4

R.M.S error of the distance from each sample surface to the average reconstructed cortical surface with and without diffeomorphic sulcal matching shown for left hemisphere. There is considerable improvement in registration even where there is an absence of landmarks (labeled as A).