A novel solid-angle tomosynthesis (SAT) scanning scheme

Abstract

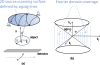
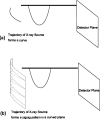
Purpose: Digital tomosynthesis (DTS) recently gained extensive research interests in both diagnostic and radiation therapy fields. Conventional DTS images are generated by scanning an x-ray source and flat-panel detector pair on opposite sides of an object, with the scanning trajectory on a one-dimensional curve. A novel tomosynthesis method named solid-angle tomosynthesis (SAT) is proposed, where the x-ray source scans on an arbitrary shaped two-dimensional surface.

Methods: An iterative algorithm in the form of total variation regulated expectation maximization is developed for SAT image reconstruction. The feasibility and effectiveness of SAT is corroborated by computer simulation studies using three-dimensional (3D) numerical phantoms including a 3D Shepp-Logan phantom and a volumetric CT image set of a human breast.

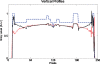
Results: SAT is able to cover more space in Fourier domain more uniformly than conventional DTS. Greater coverage and more isotropy in the frequency domain translate to fewer artifacts and more accurately restored features in the in-plane reconstruction.

Conclusions: Comparing with conventional DTS, SAT allows cone-shaped x-ray beams to project from more solid angles, thus provides more coverage in the spatial-frequency domain, resulting in better quality of reconstructed image.

Figure 1

Schematic illustration of conventional DTS technique using OBI system. According to the FST, the data collected in the image domain in (a) correspond to the shaded area enclosed by plane1 and plane3 in the Fourier domain in (b).

Figure 2

Example DTS images of a spherical object. Displayed are the in-plane reconstruction slices on the left and the cross-plane slices on the right. All results are from DTS simulations using angular scanning range of 40°, where projections are evenly spaced at a sparser interval (2°, top row) and a denser interval (0.5°, bottom row), respectively.

Figure 3

One example of SAT scheme, where the scanning surface in (a) is formed by two orthogonal arcs. Sampled Fourier region consists of two shaded revolving-door shapes, as pointed by arrows in (b).

Figure 4

Another SAT example where the scanning trajectory (defined by the zigzag lines) covers a patch of a spherical surface in (a). Sampled Fourier region corresponds to the whole space minus the two cones (upper and bottom), as pointed by arrows in (b), which is a bigger region and more isotropic than that of DTS shown in Fig. 1.

Figure 5

3D Shepp–Logan phantom used for the computer simulations (a) and central x-z slice of the phantom (b).

Figure 6

(a) The side-view of a hypothetical prone-position breast imaging system and (b) its head-on view. (c) shows a slice of a digital breast phantom, parallel to the detector plane marked by the dashed line in (b). The digital breast phantom is the CT image acquired with CT contrast, using the dedicated breast CT scanner developed at UC Davis

Figure 7

(a) illustrates conventional DTS scan using the breast imaging system depicted by Fig. 6. The x-ray source rotates around the breast on an arc at the couch level. (b) illustrates the SAT scheme where the x-ray source moves in zigzag pattern relative to the breast. The source trajectory consists of the several arcs on the cylindrical surface, with the first arc starting from the couch level.

Figure 8

Reconstructed slices of the Shepp–Logan phantom by using (a) conventional DTS, (b) two-arc SAT, and (c) zigzag SAT scanning schemes, respectively, as illustrated on the top row. The total number of projections is the same for each method.

Figure 9

Vertical profile through the center of the true object [Fig. 5b] (dashed line), the conventional DTS image [Fig. 8a] (dotted line), and the zigzag SAT image [Fig. 8c] (solid line).

Figure 10

Reconstructed breast images using DTS method (top row) and SAT method (bottom row), as described by Figs. 7a, 7b, respectively. The left column corresponds to scanning conditions of 120° arc(s) and 120 total number of projections, for both (a) DTS and (b) SAT; and the right column corresponds to 30° arc(s) and 30 projections for both (c) DTS and (d) SAT.