Kinetochores' gripping feat: conformational wave or biased diffusion?

Abstract

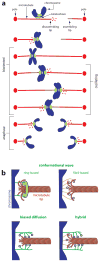
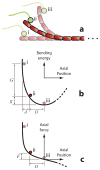
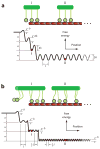
Climbing up a cliff while the rope unravels underneath your fingers does not sound like a well-planned adventure. Yet chromosomes face a similar challenge during each cell division. Their alignment and accurate segregation depends on staying attached to the assembling and disassembling tips of microtubule fibers. This coupling is mediated by kinetochores, intricate machines that attach chromosomes to an ever-changing microtubule substrate. Two models for kinetochore-microtubule coupling were proposed a quarter century ago: conformational wave and biased diffusion. These models differ in their predictions for how coupling is performed and regulated. The availability of purified kinetochore proteins has enabled biochemical and biophysical analyses of the kinetochore-microtubule interface. Here, we discuss what these studies reveal about the contributions of each model.

Figure I. Chromosome-microtubule coupling during mitosis

(a) Chromosome movement during mitosis is coupled to the growth and shortening of microtubule tips. Each duplicated chromosome has two kinetochores, one on each sister chromatid, through which they attach to the microtubules of the mitotic spindle. Initially, the kinetochores make lateral attachments to the sides of microtubules, but these attachments are converted to an end-on arrangement and thereafter the kinetochores remain persistently associated with the assembling and disassembling microtubule tips. The linkages between kinetochores and disassembling tips are sites where pulling force, directed toward the poles, is generated (i.e., these are sites where chemical energy is converted into mechanical work). When a chromosome becomes properly bioriented – with one kinetochore attached to the left side of the spindle and the other attached to the right side – pulling forces generated on one side are resisted by the connections on the other side. These opposing forces place bioriented sister kinetochores under tension, which stretches them apart from one another. In some types of cells, bioriented chromosomes oscillate back-and-forth around the spindle equator, making movements that are coupled to alternating cycles of growth and shortening of the opposing microtubules. In anaphase, after cohesion between sister chromatids is dissolved, microtubules on both sides of the spindle disassemble, thereby pulling the sisters toward opposite poles. (b) Models for chromosome-microtubule coupling. Two versions of the conformational wave mechanism are shown, one (ring-based) in which elements of the kinetochore assemble into a microtubule-encircling ring that is hooked by curling protofilaments, and another (fibril-based) where fibrillar kinetochore elements bind independently to the curling protofilaments. In either case, the curling action of the protofilaments exerts pulling force (directed rightward in the diagrams) on the chromosome. In the biased diffusion mechanism, an array of kinetochore fibers rapidly binds and unbinds the microtubule lattice at or near the tip. Thermal fluctuations of the chromosome that allow more fibers to bind (rightward movements of the chromosome in the diagram) are favored by the energy of binding those elements. This biased thermal movement produces a thermodynamic pulling force. A hybrid model is also shown, where force is produced by a combination of protofilament curling and biased thermal fluctuations.

Figure II. Energy landscape and axial force production for a curling protofilament

(a) Schematic depicting a curling protofilament (red). A segment 5 dimers in length curls out from the microtubule lattice (not shown) and drives movement of an attached kinetochore component (green). Initially, the movement (i → ii) is mainly directed radially outward from the lattice (upward in this view). Later, when a larger angle develops between the protofilament and the microtubule axis, a greater proportion of the movement (ii → iii) is directed productively towards the minus end of the microtubule (rightward in this view). (b) Bending energy stored in the protofilament versus axial position of the bound kinetochore component (i.e., its position projected onto the microtubule axis). Red dots mark energies corresponding to the conformations depicted in (a). As the protofilament relaxes from completely straight (i) into its naturally curved conformation (iii), it loses a total energy represented by g + G, and the bound kinetochore component moves axially by a distance d + D. An intermediate conformation (ii) is also shown to illustrate that a large portion, G, of the total energy is lost during the initial phase of curling, which produces comparatively less axial movement, d. (c) Relationship between axial load and axial deflection for the curled protofilament (which is essentially a semi-circular slender beam [67]). The parameter F represents the amount of opposing load that would suppress the curling by a distance D, enough to eliminate the most productive, second phase of the power stroke. Its value will depend on the effective spring constant for the curl, k = F/D, which in turn depends on the flexural rigidity, EI (see Box 1 text).

Figure III. Energy landscapes for biased diffusion

Free energy versus position (plotted as heavy black curves) for kinetochores with arrays of M = 3 microtubule-binding elements (green) on a microtubule lattice (red). Parameters w and b represent the net free energy change for detachment of a single element, and the energy change required for a single element to adopt the transition state between sites, respectively. (For simplicity, we also assume here that the transition energy for attachment of a single element to the microtubule is equivalent to b.) Red dots mark energies corresponding to the tip-bound and lattice-bound cases depicted in the cartoons. (a) Energy landscape for a rigid array whose spacing matches the spacing of the microtubule lattice. In this case, the heights of the corrugations, b, 2b, 3b, increase as more elements become bound, up to a maximum of M·b for an array that is fully bound to the lattice. The effective step size, l, is constant. (b) Energy landscape for a flexible array. In this case, the effective step sizes, l, ½l, ⅓l, decrease as more elements are bound, down to a minimum of l/M, and the corrugation heights, b, remain constant. Experiments show that the corrugation height, b, can be far smaller than the transition energy for detachment (assumed to be w+b for the landscapes shown here). Individual Ndc80 complexes, for example, exhibit lattice diffusion at a rate D_o = 0.17 μm² s⁻¹ [46], implying a very fast rate of hopping from site to site, k_hop = 2,600 s⁻¹ (= D_o/l², where l is taken as 8 nm, the longitudinal spacing of tubulin dimers in the microtubule lattice). Detachment of individual Ndc80 complexes occurs much more slowly, at k_off = 1.2 s⁻¹, implying that the transition energy for detachment must be at least 7.7 k_BT larger than b. This follows from Boltzmann’s law, which relates the energy difference, ΔU, to the ratio of rates, k_hop/k_off = exp(ΔU/k_BT), where k_BT is thermal energy (4.1 pN nm at 25° C).