Curvilinear Immersed Boundary Method for Simulating Fluid Structure Interaction with Complex 3D Rigid Bodies

Abstract

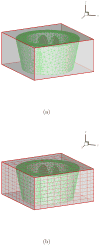
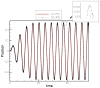
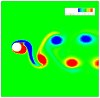
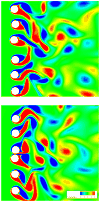
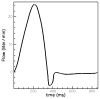
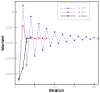
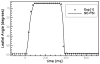
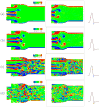
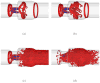
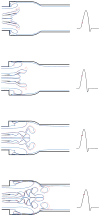
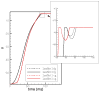
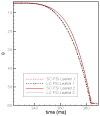
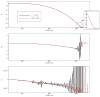
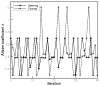
The sharp-interface CURVIB approach of Ge and Sotiropoulos [L. Ge, F. Sotiropoulos, A Numerical Method for Solving the 3D Unsteady Incompressible Navier-Stokes Equations in Curvilinear Domains with Complex Immersed Boundaries, Journal of Computational Physics 225 (2007) 1782-1809] is extended to simulate fluid structure interaction (FSI) problems involving complex 3D rigid bodies undergoing large structural displacements. The FSI solver adopts the partitioned FSI solution approach and both loose and strong coupling strategies are implemented. The interfaces between immersed bodies and the fluid are discretized with a Lagrangian grid and tracked with an explicit front-tracking approach. An efficient ray-tracing algorithm is developed to quickly identify the relationship between the background grid and the moving bodies. Numerical experiments are carried out for two FSI problems: vortex induced vibration of elastically mounted cylinders and flow through a bileaflet mechanical heart valve at physiologic conditions. For both cases the computed results are in excellent agreement with benchmark simulations and experimental measurements. The numerical experiments suggest that both the properties of the structure (mass, geometry) and the local flow conditions can play an important role in determining the stability of the FSI algorithm. Under certain conditions unconditionally unstable iteration schemes result even when strong coupling FSI is employed. For such cases, however, combining the strong-coupling iteration with under-relaxation in conjunction with the Aitken's acceleration technique is shown to effectively resolve the stability problems. A theoretical analysis is presented to explain the findings of the numerical experiments. It is shown that the ratio of the added mass to the mass of the structure as well as the sign of the local time rate of change of the force or moment imparted on the structure by the fluid determine the stability and convergence of the FSI algorithm. The stabilizing role of under-relaxation is also clarified and an upper bound of the required for stability under-relaxation coefficient is derived.

Fig. 1

The 3D BMHV geometry including the housing and the leaflets in a straight aorta (left) and the definition of leaflet angle (right). The leaflets hinge axis is placed parallel to x-axis of the global frame of reference at position (y_h, z_h) in the YZ plane.

Fig. 2

Sketch showing the idea of sharp-interface immersed boundary method.

Fig. 3

Sketch showing the ray-casting method for 2D point-in-polygon test.

Fig. 4

Sketch showing the ray-casting method for a 3D leaflet.

Fig. 5

(a) A bounding box created for a bileaflet mechanical valve. The valve is discretized with 2048 triangles. (b) The bounding box is divided into smaller control cells.

Fig. 6

An elastically mounted cylinder in the free stream

Fig. 7

Grid used for 2D vortex induced vibration (VIV) study around an elastically mounted circular cylinder.

Fig. 8

The maximum cylinder displacement as a function of U_red from present (circles) and Ahn and Kallinderis [28] (filled squares) simulations. Flow conditions: Re = 150, M_red = 2.

Fig. 9

Comparison of the cylinder kinematics obtained by LC-FSI and SC-FSI. Flow conditions: Re = 150, U_red = 4, M_red = 2.

Fig. 10

Instantaneous vorticity contours in the vicinity of the cylinder. Flow conditions: Re = 150, U_red = 4, M_red = 2.

Fig. 11

VIV of six elastically mounted cylinders. Two snapshots of out-of-plane vorticity contours. Flow conditions: Re = 100, U_red = 4, M_red = 2.

Fig. 12

The computational grid for the BMHV simulations. a)Side view showing the background curvilinear grid used to discretize the empty aorta and the unstructured mesh used to discretize the leaflets and the housing. b) Cross-sectional view of the background grid. For clarity, only every third grid is plotted.

Fig. 13

BMHV simulation. Physiological incoming flow waveform specified at the inlet.

Fig. 14

BMHV simulation, Comparison of the SC-FSI convergence history of calculated moment acting on a leaflet with constant coefficient under-relaxation and Aitken’s acceleration within a time step.

Fig. 15

BMHV simulation (fine mesh). Comparison of the calculated leaflet kinematics (solid line) with experimental observations [1] (circles).

Fig. 16

BMHV simulation on fine grid (left) compared with the PIV measurements (right) of Dasi et al [1]. Instantaneous out-of-plane vorticity contours on the mid-plane of the valve at four different time instants within a cardiac cycle. The dots on the inflow waveform shown on the right of each figure indicate the time instant during the cycle. The contour levels are identical.

Fig. 17

BMHV simulation (fine grid). Instantaneous vortical structures visualized by iso-surfaces of q-criteria at the same four time instants as of Fig. 16 within a cardiac cycle.

Fig. 18

BMHV simulation results on fine grid (solid blue lines) compared with the coarse grid (dotted red lines). Instantaneous out-of-plane vorticity iso-lines for vorticity magnitude equal to 1 on the mid-plane of the valve. The dots on the inflow waveform shown on the bottom of each figure column indicate the time instant during the cardiac cycle.

Fig. 19

BMHV simulation. Comparison of the upper and lower leaflet kinematics during the opening stage obtained by SC-FSI on the fine (black) and coarse (red) grids. fg and cg refer to fine and coarse grid, respectively.

Fig. 20

BMHV simulation. Comparison of the upper and lower leaflet kinematics during the closing stage obtained by SC-FSI and LC-FSI.

Fig. 21

BMHV simulation. Comparison of the LC-FSI vs. SC-FSI for one of the leaflets in the closing phase in terms of leaflets angle (top), angular velocity (middle), and moment coefficient (bottom).

Fig. 22

Comparison of the under-relaxation coefficient α calculated by the Aitken’s acceleration technique for SC-FSI during the early opening and closing phases.

Fig. 23

A plate rotating around a hinge in still fluid (a) and (b),(c) in a free stream. The plate is rotated by (a) a constant external moment and (b),(c) the moment exerted by the flow. The configuration and flow direction in (b) is similar to the opening phase and (c) is similar to the closing phase.