Mechanics and computational simulation of blood flow in microvessels

Abstract

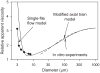
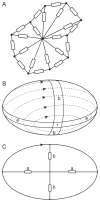
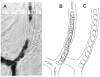
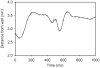
Blood is a concentrated suspension of red blood cells (RBCs). Motion and deformation of RBCs can be analyzed based on knowledge of their mechanical characteristics. Axisymmetric models for single-file motion of RBCs in capillaries yield predictions of apparent viscosity in good agreement with experimental results for diameters up to about 8 μm. Two-dimensional simulations, in which each RBC is represented as a set of interconnected viscoelastic elements, predict that off-centre RBCs in an 8-μm channel take asymmetric shapes and drift toward the centre-line. Predicted trajectories agree with observations in microvessels of the rat mesentery. An isolated RBC initially positioned near the wall of a 20-μm channel is deformed into an asymmetric shape, migrates away from the wall, and then enters a complex tumbling motion with continuous shape change. Realistic simulation of multiple interacting RBCs in microvessels remains as a major challenge.

Fig. 1

A. Human RBCs flowing in a glass tube with diameter 7 μm. B. Blood flow through a capillary in the rat mesentery with diameter approximately 7 μm. Flow is from left to right in each case.

Fig. 2

Fåhraeus-Lindqvist effect in glass tubes. Solid curve: empirical fit to experimental data [2]. Dots: theoretical predictions [16]. Dashed curve: axial-train model (see text for explanation).

Fig. 3

Variables describing geometry and stress resultants in an axisymmetric shell.

Fig. 4

A. Two-dimensional model for RBC. Rectangles represent viscoelastic elements. B, C. Relationship between internal viscous elements and membrane deformation in tank-treading. Bands of membrane (a,b) alternately shorten and elongate during tank-treading.

Fig. 5

Predicted motion and deformation of cells in an 8-μm channel. Flow rate is adjusted so that cell velocity is approximately 1.25 mm/s. Initial cell shape is a circle with radius 2.66 μm. Results are presented for cells with initial displacements 0, 0.5, 1 μm from the centre-line. A. Predicted cell shapes initially and after 50 and 100 ms. Dot on cell outline represents a node fixed in the cell. B. Observed human RBC shapes in a single glass capillary with diameter 7 μm. Three cells are shown with varying orientations and degrees of asymmetry.From Secomb et al. [19].

Fig. 6

Observations and simulations of RBC motion in rat mesenteric microvessels. A. Microvessels selected for observation. Arrow: RBC whose motion was tracked. B. Superimposed digitized outlines of vessel wall and of selected isolated cells in successive video frames at 10-ms intervals. Arrows show flow directions. C. Predicted cell shapes at 20-ms intervals. From Secomb et al. [19].

Fig. 7

Predicted RBC shapes and positions during lateral migration in a 20-μm channel, with flow driven by an imposed pressure gradient of −2000 dyn/cm³. Shear rate at the wall in the absence of particle is 200 s⁻¹and centre -line velocity is 1 mm/s. Initial cell shape is a circle with radius 2.66 μm and centre 2.8 μm from the wall. Shapes are shown at 50 -ms intervals. Times since initiation of motion are indicated in ms.

Fig. 8

Time-dependent lateral migration of a RBC in a 20-μm channel, with flow driven by an imposed pressure gradient of −2000 dyn/cm³. Distance of membrane centre of mass from wall is plotted. Symbols on curve correspond to 50-ms intervals at which cell shape is shown in Figure 7.