An improved spinning lens test to determine the stiffness of the human lens

Abstract

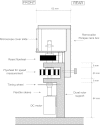
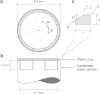
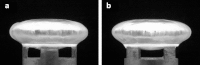
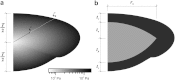
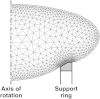
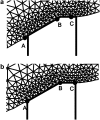
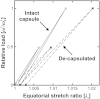
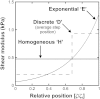
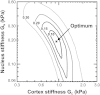
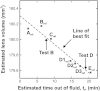
It is widely accepted that age-related changes in lens stiffness are significant for the development of presbyopia. However, precise details on the relative importance of age-related changes in the stiffness of the lens, in comparison with other potential mechanisms for the development of presbyopia, have not yet been established. One contributing factor to this uncertainty is the paucity and variability of experimental data on lens stiffness. The available published data generally indicate that stiffness varies spatially within the lens and that stiffness parameters tend to increase with age. However, considerable differences exist between these published data sets, both qualitatively and quantitatively. The current paper describes new and improved methods, based on the spinning lens approach pioneered by Fisher, R.F. (1971) 'The elastic constants of the human lens', Journal of Physiology, 212, 147-180, to make measurements on the stiffness of the human lens. These new procedures have been developed in an attempt to eliminate, or at least substantially reduce, various systematic errors in Fisher's original experiment. An improved test rig has been constructed and a new modelling procedure for determining lens stiffness parameters from observations made during the test has been devised. The experiment involves mounting a human lens on a vertical rotor so that the lens spins on its optical axis (typically at 1000 rpm). An automatic imaging system is used to capture the outline of the lens, while it is rotating, at pre-determined angular orientations. These images are used to quantify the deformations developed in the lens as a consequence of the centripetal forces induced by the rotation. Lens stiffness is inferred using axisymmetric finite element inverse analysis in which a nearly-incompressible neo-Hookean constitutive model is used to represent the mechanics of the lens. A numerical optimisation procedure is used to determine the stiffness parameters that provide a best fit between the finite element model and the experimental data. Sample results are presented for a human lens of age 33 years.

Fig. 1

Side view of the spinning lens rig drawn to scale. The three optical sensors are omitted for clarity.

Fig. 2

Timing wheel.

Fig. 3

Lens support detail; (a) plan, (b) elevation and (c) Delrin^® ring cross-section. Support ring dimensions determined from lateral calibration images collected during the test programme are a = 0.2 mm and c = 0.6164 mm. Data obtained from separate measurements made after completion of the test programme are a = 0.2105 mm, b = 0.3573 mm and c in the range 0.5201 mm–0.5841 mm.

Fig. 4

De-capsulated 33-year lens at a rotational speed of 1000 rpm. Figs. (a) and (b) show the lens at a relative angular orientation of 45°.

Fig. 5

Front view of the lens box.

Fig. 6

The target outline (dashed line) corresponding to the shape of the lens when spinning at 1000 rpm and the reference lens outline (solid line) corresponding to the shape of the lens when spinning at 70 rpm.

Fig. 7

Spatial Variation Functions. Figure (a) illustrates Model E and Figure (b) illustrates Model D. The grey scale shown is based on the optimised stiffness parameters for the 33-year lens (see Fig. 11). The dimension T is the axial thickness of the lens. The dimensions adopted for Model D model are: r_n = 3.45 mm, t_a = 1.132 mm, t_p = 1.698 mm. The dimension t_c is determined by the total axial thickness, T, of the particular lens being modelled.

Fig. 8

Reference finite element mesh for the 33-year lens.

Fig. 9

Movement of the lens relative to the support for the 33-year lens, smooth support case. The Group 1 nodes lie between Points A and B and Group 2 nodes lie between Points B and C. The location of these nodes is shown in Fig. (a) at the start of the analysis, corresponding to a stationary lens, and in Fig. (b) where the lens is spinning at 1000 rpm. In Fig. (b), the points A, B and C are seen to coincide correctly with the geometry of the support.

Fig. 10

Equatorial stretch ratio, λ_e for the 33-year lens for the test sequence given in Table 1.

Fig. 11

Optimised stiffness data for Models H, E and D. These data are plotted in terms of relative position, p_r. The shape of interface between the nucleus and cortex for Model D means that the interface does not correspond to a single value of p_r. For illustrative purposes, the interface is plotted in the figure at an average value of p_r. Shear modulus for Model H is 0.47 kPa. Parameters for Model E are α = 0.062 kPa and β = 3.02. Parameters for Model D are G_N = 0.19 kPa and G_C = 0.93 kPa.

Fig. 12

Contours of the error parameter γ_E. (Note that stiffness data are plotted on a logarithmic scale).

Fig. 13

Variation with time of the estimated lens volume for the 33-year de-capsulated lens.