Mutational effects and population dynamics during viral adaptation challenge current models
- PMID: 21041559
- PMCID: PMC3018297
- DOI: 10.1534/genetics.110.121400
Mutational effects and population dynamics during viral adaptation challenge current models
Abstract
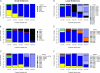
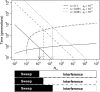
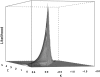
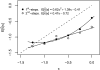
Adaptation in haploid organisms has been extensively modeled but little tested. Using a microvirid bacteriophage (ID11), we conducted serial passage adaptations at two bottleneck sizes (10(4) and 10(6)), followed by fitness assays and whole-genome sequencing of 631 individual isolates. Extensive genetic variation was observed including 22 beneficial, several nearly neutral, and several deleterious mutations. In the three large bottleneck lines, up to eight different haplotypes were observed in samples of 23 genomes from the final time point. The small bottleneck lines were less diverse. The small bottleneck lines appeared to operate near the transition between isolated selective sweeps and conditions of complex dynamics (e.g., clonal interference). The large bottleneck lines exhibited extensive interference and less stochasticity, with multiple beneficial mutations establishing on a variety of backgrounds. Several leapfrog events occurred. The distribution of first-step adaptive mutations differed significantly from the distribution of second-steps, and a surprisingly large number of second-step beneficial mutations were observed on a highly fit first-step background. Furthermore, few first-step mutations appeared as second-steps and second-steps had substantially smaller selection coefficients. Collectively, the results indicate that the fitness landscape falls between the extremes of smooth and fully uncorrelated, violating the assumptions of many current mutational landscape models.
Figures

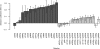
References
-
- Akaike, H., 1974. New look at statistical-model identification. IEEE Trans. Automat. Contr. Ac19 716–723.
-
- Betancourt, A. J., and J. P. Bollback, 2006. Fitness effects of beneficial mutations: the mutational landscape model in experimental evolution. Curr. Opin. Genet. Dev. 16 618–623. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

