An integrated approach to epitope analysis I: Dimensional reduction, visualization and prediction of MHC binding using amino acid principal components and regression approaches
- PMID: 21044289
- PMCID: PMC2990731
- DOI: 10.1186/1745-7580-6-7
An integrated approach to epitope analysis I: Dimensional reduction, visualization and prediction of MHC binding using amino acid principal components and regression approaches
Abstract
Background: Operation of the immune system is multivariate. Reduction of the dimensionality is essential to facilitate understanding of this complex biological system. One multi-dimensional facet of the immune system is the binding of epitopes to the MHC-I and MHC-II molecules by diverse populations of individuals. Prediction of such epitope binding is critical and several immunoinformatic strategies utilizing amino acid substitution matrices have been designed to develop predictive algorithms. Contemporaneously, computational and statistical tools have evolved to handle multivariate and megavariate analysis, but these have not been systematically deployed in prediction of MHC binding. Partial least squares analysis, principal component analysis, and associated regression techniques have become the norm in handling complex datasets in many fields. Over two decades ago Wold and colleagues showed that principal components of amino acids could be used to predict peptide binding to cellular receptors. We have applied this observation to the analysis of MHC binding, and to derivation of predictive methods applicable on a whole proteome scale.
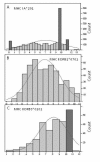
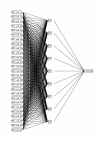
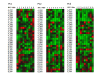
Results: We show that amino acid principal components and partial least squares approaches can be utilized to visualize the underlying physicochemical properties of the MHC binding domain by using commercially available software. We further show the application of amino acid principal components to develop both linear partial least squares and non-linear neural network regression prediction algorithms for MHC-I and MHC-II molecules. Several visualization options for the output aid in understanding the underlying physicochemical properties, enable confirmation of earlier work on the relative importance of certain peptide residues to MHC binding, and also provide new insights into differences among MHC molecules. We compared both the linear and non-linear MHC binding prediction tools to several predictive tools currently available on the Internet.
Conclusions: As opposed to the highly constrained user-interaction paradigms of web-server approaches, local computational approaches enable interactive analysis and visualization of complex multidimensional data using robust mathematical tools. Our work shows that prediction tools such as these can be constructed on the widely available JMP® platform, can operate in a spreadsheet environment on a desktop computer, and are capable of handling proteome-scale analysis with high throughput.
Figures


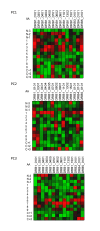
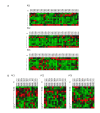

References
-
- Wold S, Sjorstrom M, Eriksson L. PLS-regression: a basic tool of chemometrics. Chemometrics and Intelligent Laboratory Systems. 2001;58:109–130. doi: 10.1016/S0169-7439(01)00155-1. - DOI
-
- Eriksson L, Johansson E, Kettaneh-Wold N, Trygg J, Wikstrom C, Wold S. Multi and Megavariate Data Analysis. Part II: Advanced Appplications and Method Extensions. 2. Umetrics Academy, Umea, Sweden; 2006.
-
- Eriksson L, Johansson E, Kettaneh-Wold N, Trygg J, Wikstrom C, Wold S. Multi and Megavariate Data Analysis. Part I: Basic Principles and Applications. 2. Umetrics Academy, Umea, Sweden; 2006.
-
- Flower DR, McSparron H, Blythe MJ, Zygouri C, Taylor D, Guan P, Wan S, Coveney PV, Walshe V, Borrow P, Doytchinova IA. Computational vaccinology: quantitative approaches. Novartis Found Symp. 2003;254:102–120. full_text. - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
