Beneficial laggards: multilevel selection, cooperative polymorphism and division of labour in threshold public good games

Abstract

Background: The origin and stability of cooperation is a hot topic in social and behavioural sciences. A complicated conundrum exists as defectors have an advantage over cooperators, whenever cooperation is costly so consequently, not cooperating pays off. In addition, the discovery that humans and some animal populations, such as lions, are polymorphic, where cooperators and defectors stably live together--while defectors are not being punished--, is even more puzzling. Here we offer a novel explanation based on a Threshold Public Good Game (PGG) that includes the interaction of individual and group level selection, where individuals can contribute to multiple collective actions, in our model group hunting and group defense.

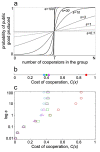
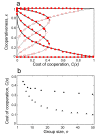
Results: Our results show that there are polymorphic equilibria in Threshold PGGs; that multi-level selection does not select for the most cooperators per group but selects those close to the optimum number of cooperators (in terms of the Threshold PGG). In particular for medium cost values division of labour evolves within the group with regard to the two types of cooperative actions (hunting vs. defense). Moreover we show evidence that spatial population structure promotes cooperation in multiple PGGs. We also demonstrate that these results apply for a wide range of non-linear benefit function types.

Conclusions: We demonstrate that cooperation can be stable in Threshold PGG, even when the proportion of so called free riders is high in the population. A fundamentally new mechanism is proposed how laggards, individuals that have a high tendency to defect during one specific group action can actually contribute to the fitness of the group, by playing part in an optimal resource allocation in Threshold Public Good Games. In general, our results show that acknowledging a multilevel selection process will open up novel explanations for collective actions.

Figure 1

The schematic representation of the relationships between the different units in the different model scenarios. Lion hunting groups (A) and human hunters (B) successfully trap large preys by encircling it, that solitary or few individuals would be unable to do so. The presented model based on these remarks, where individuals are represented by the coloured circles, which indicate their trait composition (a-c). The individuals' location in the population can be fixed in the spatially explicit model, or individuals can disperse randomly in the well-mixed model. The group (big grey circle) is composed of individuals existing at a location of certain size at that moment (grey arrow). Individuals make their contributions to the group hunting effort (small green arrows), and receive the payoff according to the rules of the game. (a) Individual competition only. A randomly chosen focal individual (dashed circle) competes either with one of its group mates in the spatially explicit model, or with a randomly picked individual from the population in the well-mixed model (blue shadings). (b) Individual and group competition. Individual competition as before, and after the focal group competes with either a neighbouring group or a random group from the population (green shading). (c) Individual and group competition with voluntary participation in the both of the group actions, such as the cooperative hunting and the competition between groups for territories. (d) In the last case individuals have two continuous traits which determine their propensity to participate in the group actions, x for the Public Good Game, and a for the group competition game, both between 0 and 1. (pictures from: classicafrica.com; gtemporium.wordpress.com).

Figure 2

The effect of s parameter on the level of cooperativeness in the population. (a) The s parameter determines the steepness, hence the shape of the sigmoid function. When s approaches ∞, the probabilistic benefit function approaches to strict deterministic step-wise function, meaning that above the threshold (T) the public good is always achieved, while below never. With decreasing s the probability of public good achievement changes from strict all or nothing to a smoother function. In the later case there is a non-zero probability of achieving the common goal even below the threshold, and also above the threshold the group can fail. (b) The position of the hysteresis point with the use of strict deterministic step-wise benefit function. (c) The effect of s (steepness of the sigmoid function) parameter on the location of the hysteresis point. The hysteresis point indicates the highest cost value for which cooperation is still a stable outcome of the game, and even a small increase in the cost would cause the collapse of this polymorphic equilibrium to defection. Below this cost value we always find cooperative equilibria. (●,○: T = 5; ■,□: T = 4; ♦,◊: T = 3; ▲, Δ: T = 2).

Figure 3

Stable and instable fix points of the model and the position of the hysteresis point for different group sizes (n). Results from numerical and individual-based (IBM) simulations show the same results. Instable fix points (dashed line for numerical simulations, open red circles for IBM simulations) separate the interior stable fix points (thick lines for numerical and filled red circles for IBM simulations) and 0 cooperativeness in the system. a, Group size (n) is 5, the threshold values are (T) 5, 4, 3, 2, 1. b, the locations of the hysteresis points (i.e. the maximal cost where cooperation still can be a stable), with different group sizes (n). (♦: T = n-1; ▲: T = n/2).

Figure 4

Equilibrium frequency of cooperators as a function of the cost of the Public Good Game (C(x)). The panels depict the results of the individual-based simulations for non-zero stable fix points (filled marks) and instable fix points (open marks). The groups are composed of 5 individuals either picked randomly from the population (a, b, c), or from the same site in the model with spatial population structure (d, e, f). In cases a, d competition occurs only between groups, in the simulations of b and e, both individuals and groups compete with each other with compulsory participation. Finally in the cases of c, f both individual and group level selection are present and participation in the group stage is voluntary. The different marks are depicted to different threshold values (●,○: T = 5; ■,□: T = 4; ♦,◊: T = 3; ▲, Δ: T = 2).

Figure 5

Simulation results for the multilevel selection model with voluntary participation. The average propensity for cooperation concerning the two kinds of group actions, the public goods game and the voluntary group competition action as a function of the two costs of cooperation (C(x) and C(a)) and the initial ratio of cooperators (x_i) in the Public Goods Game. (a) For high cost values the tendency of cooperating in both of group actions is low, (b) or there is a full cooperation in the Public Goods Game, but full defection in the group defense action. (c) If the costs of cooperation are not high, every individual cooperates in both of the group actions (x = ~1, a = ~1). (d) At the boundaries of these regions, for intermediate cost values division of labour evolves in the population (h). On graphs e.-h. each bubble illustrates the results of an individual based simulation, the size representing the average a in the population (large bubbles represent a = 1 and vice versa), and the colouring depicting the average value of x (red bubbles denote x = 1, while yellow ones denote x = 0). For the simulations we either used no initial incentive in the populations for participating in the group competition (a_i = 0) (e, g), or the simulation was started with full participation (a_i = 1) (f, h). The 5 group members were either picked randomly from the population in the well-mixed model (e, f), or from the same site in the spatially explicit model (g, h). ((a) C(x) = 0.5, C(a) = 0.5, x_i = 0, a_i = 0; (b) C(x) = 0, C(a) = 0.6, x_i = 0, a_i = 0.5; (c) C(x) = 0.2, C(a) = 0.05, x_i = 0.05, a_i = 0.2; (d) C(x) = 0.6, C(a) = 0.2, x_i = 0.6, a_i = 0.5).