Symmetry, stability, and reversibility properties of idealized confined microtubule cytoskeletons
- PMID: 21044580
- PMCID: PMC2965936
- DOI: 10.1016/j.bpj.2010.09.017
Symmetry, stability, and reversibility properties of idealized confined microtubule cytoskeletons
Abstract
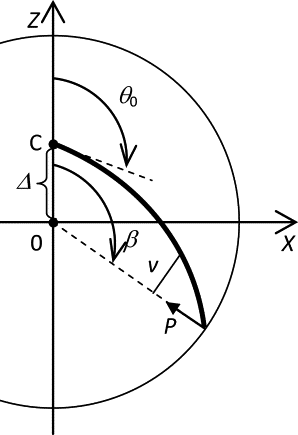
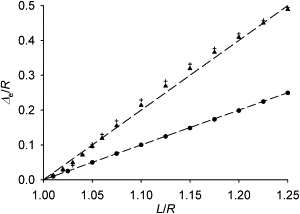
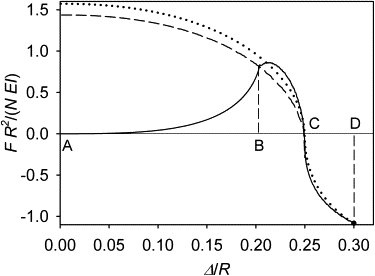
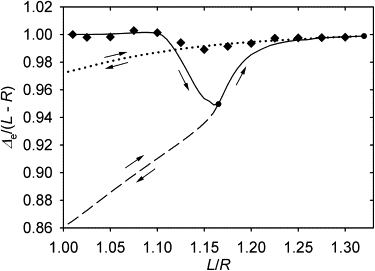
Many cell cytoskeletons include an aster of microtubules, with the centrosome serving as the focal point. The position of the centrosome within the cell is important in such directional activities as wound closure and interactions of immune cells. Here we analyzed the centrosome positioning as it is dictated by microtubule elasticity alone in a mechanical model of an intrinsically fully symmetric microtubule aster. We demonstrate that the symmetry and the central position of the centrosome are unstable. The equilibrium deviation of the centrosome from the center is approximately proportional to the difference of the microtubule length and cell radius. The proportionality coefficient is 1 in flat cells and 2 in three-dimensional cells. The loss of symmetry is irreversible, and in general, the equilibrium form of the aster exhibits memory of past perturbations. The equilibrium position of the centrosome as a function of the microtubule length exhibits hysteresis, and the history of the length variation is reflected in the aster form. These properties of the simple aster of elastic microtubules must be taken into account in the analysis of more comprehensive theoretical models, and in the design and interpretation of experiments addressing the complex process of cytoskeleton morphogenesis.
Copyright © 2010 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures

References
-
- Bray D. Garland; New York: 2000. Cell Movements: From Molecules to Motility.
-
- Kupfer A., Singer S.J. Cell biology of cytotoxic and helper T cell functions: immunofluorescence microscopic studies of single cells and cell couples. Annu. Rev. Immunol. 1989;7:309–337. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

