An atlas of gene regulatory networks reveals multiple three-gene mechanisms for interpreting morphogen gradients
- PMID: 21045819
- PMCID: PMC3010108
- DOI: 10.1038/msb.2010.74
An atlas of gene regulatory networks reveals multiple three-gene mechanisms for interpreting morphogen gradients
Abstract
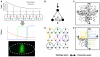
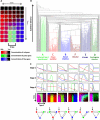
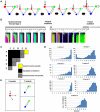
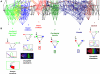
The interpretation of morphogen gradients is a pivotal concept in developmental biology, and several mechanisms have been proposed to explain how gene regulatory networks (GRNs) achieve concentration-dependent responses. However, the number of different mechanisms that may exist for cells to interpret morphogens, and the importance of design features such as feedback or local cell-cell communication, is unclear. A complete understanding of such systems will require going beyond a case-by-case analysis of real morphogen interpretation mechanisms and mapping out a complete GRN 'design space.' Here, we generate a first atlas of design space for GRNs capable of patterning a homogeneous field of cells into discrete gene expression domains by interpreting a fixed morphogen gradient. We uncover multiple very distinct mechanisms distributed discretely across the atlas, thereby expanding the repertoire of morphogen interpretation network motifs. Analyzing this diverse collection of mechanisms also allows us to predict that local cell-cell communication will rarely be responsible for the basic dose-dependent response of morphogen interpretation networks.
Conflict of interest statement
The authors declare that they have no conflict of interest.
Figures

Similar articles
-
Morphogen gradients: from generation to interpretation.Annu Rev Cell Dev Biol. 2011;27:377-407. doi: 10.1146/annurev-cellbio-092910-154148. Epub 2011 Jul 29. Annu Rev Cell Dev Biol. 2011. PMID: 21801015 Review.
-
Elucidating multi-input processing 3-node gene regulatory network topologies capable of generating striped gene expression patterns.PLoS Comput Biol. 2022 Feb 14;18(2):e1009704. doi: 10.1371/journal.pcbi.1009704. eCollection 2022 Feb. PLoS Comput Biol. 2022. PMID: 35157698 Free PMC article.
-
Mathematical model of the formation of morphogen gradients through membrane-associated non-receptors.Bull Math Biol. 2010 May;72(4):805-29. doi: 10.1007/s11538-009-9470-2. Epub 2009 Oct 31. Bull Math Biol. 2010. PMID: 19882189
-
Spatiotemporal mechanisms of morphogen gradient interpretation.Curr Opin Genet Dev. 2011 Dec;21(6):726-31. doi: 10.1016/j.gde.2011.10.002. Epub 2011 Oct 25. Curr Opin Genet Dev. 2011. PMID: 22033220 Free PMC article. Review.
-
Encoding and decoding of positional information in morphogen-dependent patterning.Curr Opin Genet Dev. 2012 Dec;22(6):553-61. doi: 10.1016/j.gde.2012.10.002. Epub 2012 Nov 28. Curr Opin Genet Dev. 2012. PMID: 23200115 Review.
Cited by
-
Finding gene network topologies for given biological function with recurrent neural network.Nat Commun. 2021 May 25;12(1):3125. doi: 10.1038/s41467-021-23420-5. Nat Commun. 2021. PMID: 34035278 Free PMC article.
-
Systems approach to developmental biology--designs for robust patterning.IET Syst Biol. 2013 Apr;7(2):38-49. doi: 10.1049/iet-syb.2012.0042. IET Syst Biol. 2013. PMID: 23847812 Free PMC article. Review.
-
Pareto evolution of gene networks: an algorithm to optimize multiple fitness objectives.Phys Biol. 2012 Oct;9(5):056001. doi: 10.1088/1478-3975/9/5/056001. Epub 2012 Aug 8. Phys Biol. 2012. PMID: 22874123 Free PMC article.
-
Genotype networks of 80 quantitative Arabidopsis thaliana phenotypes reveal phenotypic evolvability despite pervasive epistasis.PLoS Comput Biol. 2020 Aug 13;16(8):e1008082. doi: 10.1371/journal.pcbi.1008082. eCollection 2020 Aug. PLoS Comput Biol. 2020. PMID: 32790763 Free PMC article.
-
Design principles of stripe-forming motifs: the role of positive feedback.Sci Rep. 2014 May 16;4:5003. doi: 10.1038/srep05003. Sci Rep. 2014. PMID: 24830352 Free PMC article.
References
-
- Bayly RD, Ngo M, Aglyamova GV, Agarwala S (2007) Regulation of ventral midbrain patterning by Hedgehog signaling. Development 134: 2115–2124 - PubMed
-
- Briscoe J, Chen Y, Jessell TM, Struhl G (2001) A hedgehog-insensitive form of patched provides evidence for direct long-range morphogen activity of sonic hedgehog in the neural tube. Mol Cell 7: 1279–1291 - PubMed
-
- Chouard T (2008) Beneath the surface. Nature 456: 300–303 - PubMed
-
- Clyde DE, Corado MS, Wu X, Paré A, Papatsenko D, Small S (2003) A self-organizing system of repressor gradients establishes segmental complexity in Drosophila. Nature 18: 849–853 - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Miscellaneous

