A computational model of limb impedance control based on principles of internal model uncertainty
- PMID: 21049061
- PMCID: PMC2964289
- DOI: 10.1371/journal.pone.0013601
A computational model of limb impedance control based on principles of internal model uncertainty
Abstract
Efficient human motor control is characterized by an extensive use of joint impedance modulation, which is achieved by co-contracting antagonistic muscles in a way that is beneficial to the specific task. While there is much experimental evidence available that the nervous system employs such strategies, no generally-valid computational model of impedance control derived from first principles has been proposed so far. Here we develop a new impedance control model for antagonistic limb systems which is based on a minimization of uncertainties in the internal model predictions. In contrast to previously proposed models, our framework predicts a wide range of impedance control patterns, during stationary and adaptive tasks. This indicates that many well-known impedance control phenomena naturally emerge from the first principles of a stochastic optimization process that minimizes for internal model prediction uncertainties, along with energy and accuracy demands. The insights from this computational model could be used to interpret existing experimental impedance control data from the viewpoint of optimality or could even govern the design of future experiments based on principles of internal model uncertainty.
Conflict of interest statement
Figures


 . The colors represent the noise variance as a function of muscle activations, whereas the dark lines represent muscle activations that exert the same joint torque computed for joint angle position
. The colors represent the noise variance as a function of muscle activations, whereas the dark lines represent muscle activations that exert the same joint torque computed for joint angle position  . (a) Only muscle
. (a) Only muscle  is activated, producing
is activated, producing  Nm joint torque with a Gaussian kinematic variability of
Nm joint torque with a Gaussian kinematic variability of  . (b) The same torque with higher co-contraction produces significantly higher kinematic variability of
. (b) The same torque with higher co-contraction produces significantly higher kinematic variability of  under standard SDN. (c) Same conditions as in (a) in the case where only muscle
under standard SDN. (c) Same conditions as in (a) in the case where only muscle  is activated. In contrast to (b) the extended SDN in (d) favors co-contraction leading to smaller kinematic variability of
is activated. In contrast to (b) the extended SDN in (d) favors co-contraction leading to smaller kinematic variability of  and to more stable reaching.
and to more stable reaching.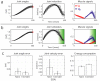




Similar articles
-
Rational selection of experimental readout and intervention sites for reducing uncertainties in computational model predictions.BMC Bioinformatics. 2015 Jan 16;16:13. doi: 10.1186/s12859-014-0436-5. BMC Bioinformatics. 2015. PMID: 25592474 Free PMC article.
-
Stochastic optimal open-loop control as a theory of force and impedance planning via muscle co-contraction.PLoS Comput Biol. 2020 Feb 28;16(2):e1007414. doi: 10.1371/journal.pcbi.1007414. eCollection 2020 Feb. PLoS Comput Biol. 2020. PMID: 32109941 Free PMC article.
-
Uncertainty analysis of Altantic salmon fish scale's acoustic impedance using 30 MHz C-Scan measurements.Ultrasonics. 2024 Aug;142:107360. doi: 10.1016/j.ultras.2024.107360. Epub 2024 Jun 6. Ultrasonics. 2024. PMID: 38924961
-
Computational principles of sensorimotor control that minimize uncertainty and variability.J Physiol. 2007 Jan 15;578(Pt 2):387-96. doi: 10.1113/jphysiol.2006.120121. Epub 2006 Sep 28. J Physiol. 2007. PMID: 17008369 Free PMC article. Review.
-
Dynamics systems vs. optimal control--a unifying view.Prog Brain Res. 2007;165:425-45. doi: 10.1016/S0079-6123(06)65027-9. Prog Brain Res. 2007. PMID: 17925262 Review.
Cited by
-
The impact of age-related increase in passive muscle stiffness on simulated upper limb reaching.R Soc Open Sci. 2023 Feb 8;10(2):221453. doi: 10.1098/rsos.221453. eCollection 2023 Feb. R Soc Open Sci. 2023. PMID: 36778951 Free PMC article.
-
Counteracting uncertainty: exploring the impact of anxiety on updating predictions about environmental states.Biol Cybern. 2025 Feb 20;119(2-3):8. doi: 10.1007/s00422-025-01006-4. Biol Cybern. 2025. PMID: 39976741 Free PMC article.
-
An examination of the generalizability of motor costs.PLoS One. 2013;8(1):e53759. doi: 10.1371/journal.pone.0053759. Epub 2013 Jan 14. PLoS One. 2013. PMID: 23341994 Free PMC article.
-
Reward-Based Improvements in Motor Control Are Driven by Multiple Error-Reducing Mechanisms.J Neurosci. 2020 Apr 29;40(18):3604-3620. doi: 10.1523/JNEUROSCI.2646-19.2020. Epub 2020 Mar 31. J Neurosci. 2020. PMID: 32234779 Free PMC article.
-
A Review of Sensory Feedback in Upper-Limb Prostheses From the Perspective of Human Motor Control.Front Neurosci. 2020 Jun 23;14:345. doi: 10.3389/fnins.2020.00345. eCollection 2020. Front Neurosci. 2020. PMID: 32655344 Free PMC article. Review.
References
-
- Hogan N. Adaptive control of mechanical impedance by coactivation of antagonist muscles. IEEE Trans Automat Contr. 1984;29:681–690.
-
- Burdet E, Osu R, Franklin DW, Milner TE, Kawato M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature. 2001;414:446–449. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

