A simplified formula for quantification of the probability of deterministic assignments in permuted block randomization

Abstract

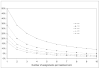
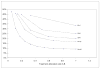
Open label and single blinded randomized controlled clinical trials are vulnerable to selection bias when the next treatment assignment is predictable based on the randomization algorithm and the preceding assignment history. While treatment predictability is an issue for all constrained randomization algorithms, deterministic assignments are unique to permuted block randomization. Deterministic assignments may lead to treatment predictability with certainty and selection bias, which could inflate the type I error and hurts the validity of trial results. It is important to accurately evaluate the probability of deterministic assignments in permuted block randomization, so proper protection measures can be implemented. For trials with number of treatment arms T = 2 and a balance block size B = 2m, Matts and Lachin indicated that the probability of deterministic assignment is 1m+1. For more general situations, with T ≥ 2 and a block size B=∑j=1Tmj, Dupin-Spriet provided a formula, which can be written as 1B∑j=1T∑i=1mj∏k=1imj-k+1B-k+1. This formula involves extensive calculation in evaluation. In this paper, we simplified this formula to 1B∑j=1TmjB-mj+1 for general scenarios and 1B-m+1 for trials with a balanced allocation. Through mathematical induction we show the equivalence of the formulas. While the new formula is numerically equivalent to Dupin-Spriet's formula, the simple format not only is easier for evaluation, but also is clearer in describing the impact of parameters T and m(i) on the probability of deterministic assignments.

Figure 1

Proportion of determinative assignment in permuted block randomizaiton for balanced trials

Figure 2

Treatment allocation ratio v.s. probability of deterministic assignment for two-arm trials