An introduction to NMR-based approaches for measuring protein dynamics
- PMID: 21059410
- PMCID: PMC3061256
- DOI: 10.1016/j.bbapap.2010.10.012
An introduction to NMR-based approaches for measuring protein dynamics
Abstract
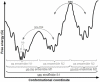
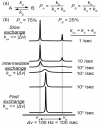
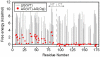
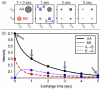
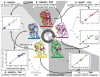
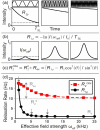
Proteins are inherently flexible at ambient temperature. At equilibrium, they are characterized by a set of conformations that undergo continuous exchange within a hierarchy of spatial and temporal scales ranging from nanometers to micrometers and femtoseconds to hours. Dynamic properties of proteins are essential for describing the structural bases of their biological functions including catalysis, binding, regulation and cellular structure. Nuclear magnetic resonance (NMR) spectroscopy represents a powerful technique for measuring these essential features of proteins. Here we provide an introduction to NMR-based approaches for studying protein dynamics, highlighting eight distinct methods with recent examples, contextualized within a common experimental and analytical framework. The selected methods are (1) Real-time NMR, (2) Exchange spectroscopy, (3) Lineshape analysis, (4) CPMG relaxation dispersion, (5) Rotating frame relaxation dispersion, (6) Nuclear spin relaxation, (7) Residual dipolar coupling, (8) Paramagnetic relaxation enhancement. This article is part of a Special Issue entitled: Protein Dynamics: Experimental and Computational Approaches.
Copyright © 2010 Elsevier B.V. All rights reserved.
Figures

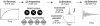

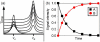



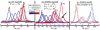
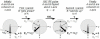









References
-
- Henzler-Wildman K, Kern D. Dynamic personalities of proteins. Nature. 2007:964–972. - PubMed
-
- Boehr DD, Dyson HJ, Wright PE. An nmr perspective on enzyme dynamics. Chem. Rev. 2006:3055–3079. - PubMed
-
- Kamerzell TJ, Middaugh CR. The complex inter-relationships between protein flexibility and stability. J Pharm Sci. 2008:3494–3517. - PubMed
-
- Loria JP, Berlow RB, Watt ED. Characterization of enzyme motions by solution nmr relaxation dispersion. Acc. Chem. Res. 2008:214–221. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

