A dynamic dose-response model to account for exposure patterns in risk assessment: a case study in inhalation anthrax
- PMID: 21068030
- PMCID: PMC3061128
- DOI: 10.1098/rsif.2010.0491
A dynamic dose-response model to account for exposure patterns in risk assessment: a case study in inhalation anthrax
Abstract
The most commonly used dose-response models implicitly assume that accumulation of dose is a time-independent process where each pathogen has a fixed risk of initiating infection. Immune particle neutralization of pathogens, however, may create strong time dependence; i.e. temporally clustered pathogens have a better chance of overwhelming the immune particles than pathogen exposures that occur at lower levels for longer periods of time. In environmental transmission systems, we expect different routes of transmission to elicit different dose-timing patterns and thus potentially different realizations of risk. We present a dose-response model that captures time dependence in a manner that incorporates the dynamics of initial immune response. We then demonstrate the parameter estimation of our model in a dose-response survival analysis using empirical time-series data of inhalational anthrax in monkeys in which we find slight dose-timing effects. Future dose-response experiments should include varying the time pattern of exposure in addition to varying the total doses delivered. Ultimately, the dynamic dose-response paradigm presented here will improve modelling of environmental transmission systems where different systems have different time patterns of exposure.
Figures
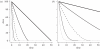
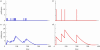
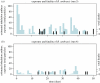
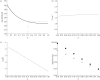
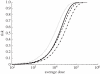
 ; dashed line, Brachman results α = 1; dash-dotted line, Brachman results [15]; dotted line, Brookmeyer et al. [10].
; dashed line, Brachman results α = 1; dash-dotted line, Brachman results [15]; dotted line, Brookmeyer et al. [10].References
-
- Haas C. N., Rose J. B., Gerba C. P. 1999. Quantitative microbial risk assessment. New York, NY: John Wiley
-
- Haas C. N. 1983. Estimation of risk due to low doses of microorganisms: a comparison of alternative methodologies. Am. J. Epidemiol. 118, 1097–1100 - PubMed
-
- Haas C. N. 1996. How to average microbial densities to characterize risk. Water Res. 30, 1036–103810.1016/0043-1354(95)00228-6 (doi:10.1016/0043-1354(95)00228-6) - DOI - DOI
-
- Pujol J. M., Eisenberg J. E., Haas C. N., Koopman J. S. 2009. The effect of ongoing exposure dynamics in dose response relationships. PLoS Comput. Biol. 5, e1000399.10.1371/journal.pcbi.1000399 (doi:10.1371/journal.pcbi.1000399) - DOI - DOI - PMC - PubMed
Publication types
MeSH terms
Supplementary concepts
LinkOut - more resources
Full Text Sources

