Efficient parallel and out of core algorithms for constructing large bi-directed de Bruijn graphs

Abstract

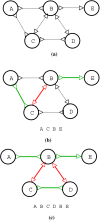
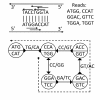
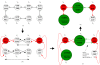
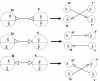
Background: Assembling genomic sequences from a set of overlapping reads is one of the most fundamental problems in computational biology. Algorithms addressing the assembly problem fall into two broad categories - based on the data structures which they employ. The first class uses an overlap/string graph and the second type uses a de Bruijn graph. However with the recent advances in short read sequencing technology, de Bruijn graph based algorithms seem to play a vital role in practice. Efficient algorithms for building these massive de Bruijn graphs are very essential in large sequencing projects based on short reads. In an earlier work, an O(n/p) time parallel algorithm has been given for this problem. Here n is the size of the input and p is the number of processors. This algorithm enumerates all possible bi-directed edges which can overlap with a node and ends up generating Θ(nΣ) messages (Σ being the size of the alphabet).

Results: In this paper we present a Θ(n/p) time parallel algorithm with a communication complexity that is equal to that of parallel sorting and is not sensitive to Σ. The generality of our algorithm makes it very easy to extend it even to the out-of-core model and in this case it has an optimal I/O complexity of Θ(nlog(n/B)Blog(M/B)) (M being the main memory size and B being the size of the disk block). We demonstrate the scalability of our parallel algorithm on a SGI/Altix computer. A comparison of our algorithm with the previous approaches reveals that our algorithm is faster--both asymptotically and practically. We demonstrate the scalability of our sequential out-of-core algorithm by comparing it with the algorithm used by VELVET to build the bi-directed de Bruijn graph. Our experiments reveal that our algorithm can build the graph with a constant amount of memory, which clearly outperforms VELVET. We also provide efficient algorithms for the bi-directed chain compaction problem.

Conclusions: The bi-directed de Bruijn graph is a fundamental data structure for any sequence assembly program based on Eulerian approach. Our algorithms for constructing Bi-directed de Bruijn graphs are efficient in parallel and out of core settings. These algorithms can be used in building large scale bi-directed de Bruijn graphs. Furthermore, our algorithms do not employ any all-to-all communications in a parallel setting and perform better than the prior algorithms. Finally our out-of-core algorithm is extremely memory efficient and can replace the existing graph construction algorithm in VELVET.

Figure 1

This figure illustrates bi-directed between two nodes in a bi-directed graph. (a) Shows a bi-directed graph with five nodes {A, B, C, D, E}. (b) The alternating green, red edges show a path between node A and E. (c) Shows two valid bi-directed walks from node A to E, the first path is {A, B, E} and the second path is {A, B, C, D, B, E}, this also shows that the bi-directed path may not be simple and can contain repeating nodes - in this case node B.

Figure 2

A simple example of the bi-directed de Bruijn graph of order k = 3 from a set of reads ATGG,CCAT,GGAC,GTTC, TGGA and TGGT observed from a DNA sequence ATGGACCAT and its reverse complement ATGGTCCAT. The dashed line shows one bi-directed walk which can reconstruct the original fragment.

Figure 3

The red nodes in Figure 3(b) indicate the nodes in the set V' (STEP-1), similar red colored edges indicate the edges in E'. After list ranking (STEP-3) we will have four maximal chains as follows, $(Y_2^{-},Y_3^{+}),(Y_3^{-},Y_2^{+}),(X_1^{-},X_2^{+},X_3^{-})(X_3^{+},X_2^{-},X_1^{+})$. Now if we stick to the convention described in STEP-5 we renumber the new node corresponding to the chains $(Y_2^{-},Y_3^{+}),(Y_3^{-},Y_2^{+})$ as Y₂. As a result the edges $(Y_3^{+},Y_4^{-})$ and $(Y_4^{+},Y_3^{-})$ are updated (shown in green in Figure 3(c)) as $(Y_2^{-},Y_4^{-})$ and $(Y_4^{+},Y_2^{+})$ Finally the directed edges are replaced with bi-directed edges in Figure 3(d).

Figure 4

An example illustrating problems with pointer jumping on bi-directed chains. The green colored arcs indicate valid pointer jumps, however the red colored arcs create cyclic loops and will create problems in the next pointer jumping operation.

Figure 5

An illustration of the ListRankingTransform which replaces every bi-directed edge with a pair of directed edges as shown here.

Figure 6

Proof that ListRankingTransform preserves bi-directed walk in the original graph.

Figure 7

This figure illustrates the subtle differences between internal graph representation of velvet and the bi-directed graph. (a) de Bruijn graph representation in velvet for the read fragment above, note velvet keeps track of only the first amino-acid symbol from the forward and reverse compliments. (b) bi-directed graph representation for the same read fragment.