Disentangling the functional roles of morphology and motion in the swimming of fish

Abstract

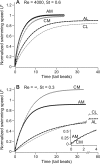
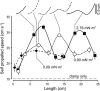
In fishes the shape of the body and the swimming mode generally are correlated. Slender-bodied fishes such as eels, lampreys, and many sharks tend to swim in the anguilliform mode, in which much of the body undulates at high amplitude. Fishes with broad tails and a narrow caudal peduncle, in contrast, tend to swim in the carangiform mode, in which the tail undulates at high amplitude. Such fishes also tend to have different wake structures. Carangiform swimmers generally produce two staggered vortices per tail beat and a strong downstream jet, while anguilliform swimmers produce a more complex wake, containing at least two pairs of vortices per tail beat and relatively little downstream flow. Are these differences a result of the different swimming modes or of the different body shapes, or both? Disentangling the functional roles requires a multipronged approach, using experiments on live fishes as well as computational simulations and physical models. We present experimental results from swimming eels (anguilliform), bluegill sunfish (carangiform), and rainbow trout (subcarangiform) that demonstrate differences in the wakes and in swimming performance. The swimming of mackerel and lamprey was also simulated computationally with realistic body shapes and both swimming modes: the normal carangiform mackerel and anguilliform lamprey, then an anguilliform mackerel and carangiform lamprey. The gross structure of simulated wakes (single versus double vortex row) depended strongly on Strouhal number, while body shape influenced the complexity of the vortex row, and the swimming mode had the weakest effect. Performance was affected even by small differences in the wakes: both experimental and computational results indicate that anguilliform swimmers are more efficient at lower swimming speeds, while carangiform swimmers are more efficient at high speed. At high Reynolds number, the lamprey-shaped swimmer produced a more complex wake than the mackerel-shaped swimmer, similar to the experimental results. Finally, we show results from a simple physical model of a flapping fin, using fins of different flexural stiffness. When actuated in the same way, fins of different stiffnesses propel themselves at different speeds with different kinematics. Future experimental and computational work will need to consider the mechanisms underlying production of the anguilliform and carangiform swimming modes, because anguilliform swimmers tend to be less stiff, in general, than are carangiform swimmers.

Fig. 1

Differences in body shape and swimming mode. (A) Eel body shape from the side and (B) anguilliform swimming mode from the top. (C) Mackerel body shape and (D) carangiform swimming mode. Kinematics panels (B and D) show forward progression at equally spaced time intervals through a tail beat cycle during swimming at ∼1.8 l s⁻¹. Scale bars are 2 cm. After Lauder and Tytell (2006); data on mackerel modified from Donley and Dickson (2000).

Fig. 2

Example of wakes of swimming bluegill sunfish and eels. Panels show horizontal planes near the fishes’ tails. Speed and direction of flow are shown by arrows and magnitude of vorticity by shades of gray. The fishes’ tails are shown in gray on the left. Vortices are numbered by the half tail beat in which each was shed. (A) A carangiform swimmer, the bluegill sunfish, Lepomis macrochirus), swimming at 1.70 l s⁻¹. Only one vortex is shed per half tail beat. (B) An anguilliform swimmer, the American eel, A. rostrata, swimming at 1.34 l s⁻¹. Note that two vortices are shed per half tail beat. The scale bars and scale vectors are the same for both panels, but the vorticity scales are different.

Fig. 3

Wake power coefficients for three different fishes swimming at a range of speeds. Relative to their body size, eels waste the smallest amount of energy producing a wake, while bluegill sunfish waste much more energy. Wakes of trout contain relatively little energy, but only at the highest swimming speed. Modified from Tytell (2007).

Fig. 4

Simulated swimming modes and body shapes. (A) Midline tracings of carangiform and anguilliform swimming motions, seen from above. Amplitudes are to scale. Carangiform kinematics from Videler and Hess (1984); anguilliform kinematics from Hultmark et al. (2007). Note that true eels often swim with less motion of the head than do lampreys. (B) Side views of the bodies of mackerel and lamprey. The bodies include only the caudal fins; other fins are neglected. (C) Plots of all combinations of shape and kinematics with the corresponding abbreviations.

Fig. 5

Simulated wakes differ primarily as a function of St. Tables show the wake type after a steady swimming speed has been reached. (A) Lamprey body and anguilliform swimming mode; (B) Mackerel body and carangiform swimming mode. Types of wakes: open circle, single row; two filled circles, double row; two open circles, transition between single and double row. Transitional wakes start off as a single row, then, further downstream in the wake, transition to a double row. Example of wakes under steady-state conditions for the anguilliform lamprey at Re = 4000 and (C) St = 0.2, single row; (D) St = 0.3, transitional; and (E) St = 0.6, double row, are shown in the lower panels. Note that most of these cases are not self-propelled; the net force on the swimmer may be not equal to 0. Data from Borazjani and Sotiropoulos (2008, 2009).

Fig. 6

Relative axial force for the tethered swimmers as a function of St. Axial force is scaled by the rigid-body drag for each body shape for Re = 300 and 4000. For the Re = ∞ case, the rigid-body drag is zero; for comparison, the forces in this case are normalized by the rigid-body drag at Re = 4000. The carangiform mackerel (CM) is shown with filled symbols and solid lines for each Re (filled diamond, filled circle, and filled square, for Re = 300, 4000, and ∞, respectively), while the anguilliform lamprey (AL) is shown with open symbols and broken lines (open diamond, open circle, and open square, for Re = 300, 4000, and ∞, respectively). Inset shows St₀, the St at which the relative axial force is zero (i.e., the swimmer is self-propelled) for each Re.

Fig. 7

Structure of the wake depends primarily on Re₀, St₀ and only secondarily on body shape or swimming mode. Panels show horizontal planes through the computational domain for all four combinations of body shape and swimming mode. Magnitude of vorticity is shown with shades of gray. Left column, Re₀ = 4000, St₀ = 0.6; right column, Re₀ = ∞, St₀ = 0.3. A, E, anguilliform lamprey; B, F, carangiform lamprey; C, G, anguilliform mackerel; and D, H, carangiform mackerel.

Fig. 8

Simulated swimmers shaped like mackerel always swim fastest, while those with anguilliform kinematics swim faster at low Re, St and slower at high Re, St. Normalized swimming speed is plotted against time in tail beats. Mackerels’ body shapes are shown with solid lines, and lampreys' body shapes with broken lines. Anguilliform swimmers are shown with thick lines and carangiform swimmers with thin lines. Abbreviations: CM, carangiform mackerel; AM, anguilliform mackerel; AL, anguilliform lamprey; CL, carangiform lamprey. (A) Re = 4000, St = 0.6 case. (B) Re = ∞, St = 0.3 case. Note the break in the time axis to show the steady speeds for the lamprey-shaped swimmer. Inset shows early times for the AM and CM swimmers.

Fig. 9

Flow speed at which the net force is zero (referred to as ‘self-propelled speed’; see text for details) for homogeneous flexible foils of different length and flexural stiffness. Traces show self-propelled speed plotted against foil length for flexural stiffness 2.76 mN m² (filled square), 0.90 mN m² (open circle), and 0.09 mN m² (filled diamond). Also shown is the self-propelled speed of the clamp that holds the foils on its own (dashed line). Foil height is 6.85 cm in all cases and they are all driven with a ± 1 cm heave motion at the leading edge. Top panel shows the maximum amplitude as a function of position along the foil from the leading edge to the trailing edge for several points, as examples.