The statistical mechanics of a polygenic character under stabilizing selection, mutation and drift

Abstract

By exploiting an analogy between population genetics and statistical mechanics, we study the evolution of a polygenic trait under stabilizing selection, mutation and genetic drift. This requires us to track only four macroscopic variables, instead of the distribution of all the allele frequencies that influence the trait. These macroscopic variables are the expectations of: the trait mean and its square, the genetic variance, and of a measure of heterozygosity, and are derived from a generating function that is in turn derived by maximizing an entropy measure. These four macroscopics are enough to accurately describe the dynamics of the trait mean and of its genetic variance (and in principle of any other quantity). Unlike previous approaches that were based on an infinite series of moments or cumulants, which had to be truncated arbitrarily, our calculations provide a well-defined approximation procedure. We apply the framework to abrupt and gradual changes in the optimum, as well as to changes in the strength of stabilizing selection. Our approximations are surprisingly accurate, even for systems with as few as five loci. We find that when the effects of drift are included, the expected genetic variance is hardly altered by directional selection, even though it fluctuates in any particular instance. We also find hysteresis, showing that even after averaging over the microscopic variables, the macroscopic trajectories retain a memory of the underlying genetic states.

Figure 1.

(a) Allele frequencies, (b) trait mean and (c) genetic variance plotted against time. A population is initially at equilibrium with stabilizing selection s = 0.05 towards z_opt = 0 acting on an additive trait, with n = 100 loci of effect γ = 1; the mutation rate is μ = 0.002 per locus, which maintains a genetic variance of ν = 4nμγs = 16. The optimum then shifts abruptly to z_opt = 20, and the mean responds almost immediately (b). The variance increases abruptly (c) as, the allele frequencies at all the ‘−’ loci increase substantially (d). However, this new state is unstable, and slight variations in the initial conditions cause some loci to shift down, and some to shift up. As a result, the genetic variance returns to its original value. The lower row shows snapshots of allele frequencies at times (d) 0, (e) 800 and (f) 3000 generations.

Figure 2.

Evolutionary dynamics when the optimum changes abruptly, shifted at time t = 0 from −0.75 to 0.75 (which corresponds to Nβ = −2.5 to Nβ = 2.5, see (c)). The trait consists of n = 5 loci of equal effect. Expectations (dashed lines) of (a) a polygenic trait and (b) its genetic variance. The grey regions cover ± the standard error (root mean squared deviation of the variance of the macroscopics). The change in the genetic variance is at most of 4.85% of the initial value, while its s.e. is 20.5%. The grey lines are averages of the numerical realizations (with population size of N = 100; 1000 replicas were employed). The goodness of fit (one tail chi-square with 51 d.f.) accepts the null hypothesis (the simulation points are random samples of the SM distributions) in both cases: (a) z = −0.058,p − 0.68; the maximum deviation is 12.19% of the standard error (0.47); (b) z = 0.12, p = 0.40; the maximum deviation is 18.27% of the standard error (0.31). (c–f) Evolution of the local forces. Note the short range of change on (d–f), these forces remain practically constant. Nλ = −1.0, Nσ = −5 and Nμ = 0.3.

Figure 3.

Evolutionary dynamics when the optimum changes abruptly, shifted at time t = 0 from −5 to 5 (which corresponds to Nβ = ±10, that is about 5% of the total range; see (c)). The trait consists of n = 100 loci of equal effect. Expectations (dashed lines) of (a) a polygenic trait and (b) its genetic variance. The grey regions cover ± the standard error (root mean squared deviation of the variance of the macroscopics). The change in the genetic variance is at most of 0.4% of the initial value, while its standard error is 10.3%. The grey lines are averages of the numerical realizations (with N = 100; 500 replicas were employed). The goodness of fit (151 d.f.) accepts the null hypothesis in both cases: (a) z = −1.14, p = 0.086; the maximum deviation is 26.5% of the standard error (0.50); (b) z = 0.18, p = 0.03; the maximum deviation is 22.19% of the standard error (1.41). (c–f) Evolution of the local forces. Note the short range of change on (d–f), these forces remain practically constant. Nλ = −1.0, Nσ = −4 and Nμ = 0.5. Otherwise as in figure 2.

Figure 4.

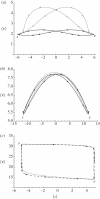
Marginal distribution of frequencies of an allele. (a) Changing the intensity of selection over the trait modulates the height of the adaptive peaks (other things being equal, Nσ = −3.0) resulting in pronounced changes in the expectation of the trait mean but with weak changes (even a relatively constant value) of the expectation of the genetic variance. Solid line: Nβ = 2.5, , 〈ν〉 = 1.12. Dashed line: Nβ = 0 . Dotted line: Nβ = −2.5, , . (b) Changing the intensity of selection over the genetic variance modulates the position of the adaptive peaks (other things being equal, Nβ = 2.5), resulting in pronounced changes in the expectation of the genetic variance, but with weak changes on the expectation of the trait mean. Dotted line: Nσ = 0, , 〈ν〉 = 8.04. Short-dashed line: Nσ = −1, , . Large-dashed line: Nσ =− 4, , . Solid line: Nσ = −10, , . In all cases Nμ = 0.5, Nλ = −1.0, and the trait is composed of 20 loci of equal effects.

Figure 5.

Evolutionary dynamics when the optimum moves gradually from −5 to 5 (which corresponds to Nβ = ±10, see (c), dotted line) at a rate of 510⁻³ units per generation. The trait consists of n = 100 loci of equal effect. Expectations (dashed lines) of (a) a polygenic trait and (b) its genetic variance. The grey regions cover ± the standard error (root mean squared deviation of the variance of the macroscopics). The grey lines are averages of the numerical realizations (with N = 100; 500 replicas were employed). The goodness of fit (151 d.f.) rejects the null hypothesis for the trait mean, and accepts it for the genetic variance: (a) z = −0.21, p = 0.009; however, the maximum deviation is 37.31% of the standard error (0.50); (b) z = 0.067, p = 0.41; the maximum deviation is 15.94% of the standard error (1.41). (c–f) Evolution of the local forces. Note the short range of change on (d–f), these forces remain practically constant. Nλ = −1, Nσ = −4, Nμ = 0.5. Otherwise as in figure 2.

Figure 6.

Evolutionary dynamics when the optimum moves gradually from −12 to 12 (which corresponds to Nβ = ± 48, 60% of the total range; see (c), dotted line) at a rate of 5 × 10⁻³ units per generation. The trait consists of n = 20 loci of equal effect. Expectations (dashed lines) of (a) a polygenic trait and (b) its genetic variance. The grey regions cover ± the standard error (root mean squared deviation of the variance of the macroscopics). The grey lines are averages of the numerical realizations (with N = 100; 500 replicas were employed). The goodness of fit (101 d.f.) rejects the null hypothesis for the trait mean, and accepts it for the genetic variance: (a) z = −0.64, p< 10^{− 9}; the maximum deviation is 171% of the standard error (0.36); (b) z = 0.06, p = 0.54; the maximum deviation is 41% of the standard error (0.69). (c–f) Evolution of the local forces. Note the short range of change on (d–f), these forces remain practically constant. Nλ = −2, Nσ = −2, Nμ = 0.5. Otherwise as in figure 2.

Figure 7.

Evolutionary dynamics when the optimum changes abruptly, shifted at time t = 0 from −5 to 5 (which corresponds to Nβ = ±10, see (c)), and simultaneously, selection against the genetic variance is increased from Nσ = −1 to Nσ = −5. The trait consists of n = 100 loci of equal effect. Expectations (dashed lines) of (a) a polygenic trait and (b) its genetic variance. The grey regions cover ± s.e. (root mean squared deviation of the variance of the macroscopics). The change in the genetic variance is at most of 0.4% of the initial value, while its standard error is 10.3% . The grey lines are averages of the numerical realizations (with N = 100; 500 replicas were employed). The goodness of fit (151 d.f.) accepts the null hypothesis for the trait mean, but rejects it for the genetic variance: (a) z =− 0.011, p − 0.87; the maximum deviation is 17.19% of the standard error (0.50); (b) z = 0.28, p< 10⁻⁴; the maximum deviation is 39.77% of the standard error (1.37). (c–f) Evolution of the local forces. Note the short range of change on (d–f), these forces remain practically constant. Nλ = −1, Nμ = 0.3. Otherwise as in figure 2.

Figure 8.

Hysteresis on the evolutionary dynamics of a trait that consists of n = 100 loci of equal effect. (a) Abrupt change in the optimum (Nβ =±12, Nσ = −15, Nλ = −1, Nμ = 0.7). (b) Moving optimum (Nβ = ±10, Nλ = −1, Nσ = −4, Nμ = 0.5; as in figure 3). (c) Abrupt change in the optimum and selection against the genetic variance (Nβ = ±12, Nσ = −1 → − 5, Nλ = −1, Nμ = 0.3; as in figure 7). The arrows indicate the direction of evolution, which start at the points s, ending at the point e, and then backwards, that is when the forces that changed are switched back. The black lines are the SM predictions, and the grey lines, averages from the simulations (population size N = 100; averages over 500 replicas). In all cases, the paths on both directions do not overlap, showing that the macroscopic states depend on the path.