The importance of structured noise in the generation of self-organizing tissue patterns through contact-mediated cell-cell signalling
- PMID: 21084342
- PMCID: PMC3104346
- DOI: 10.1098/rsif.2010.0488
The importance of structured noise in the generation of self-organizing tissue patterns through contact-mediated cell-cell signalling
Abstract
Lateral inhibition provides the basis for a self-organizing patterning system in which distinct cell states emerge from an otherwise uniform field of cells. The development of the microchaete bristle pattern on the notum of the fruitfly, Drosophila melanogaster, has long served as a popular model of this process. We recently showed that this bristle pattern depends upon a population of dynamic, basal actin-based filopodia, which span multiple cell diameters. These protrusions establish transient signalling contacts between non-neighbouring cells, generating a type of structured noise that helps to yield a well-ordered and spaced pattern of bristles. Here, we develop a general model of protrusion-based patterning to analyse the role of noise in this process. Using a simple asynchronous cellular automata rule-based model we show that this type of structured noise drives the gradual refinement of lateral inhibition-mediated patterning, as the system moves towards a stable configuration in which cells expressing the inhibitory signal are near-optimally packed. By analysing the effects of introducing thresholds required for signal detection in this model of lateral inhibition, our study shows how filopodia-mediated cell-cell communication can generate complex patterns of spots and stripes, which, in the presence of signalling noise, align themselves across a patterning field. Thus, intermittent protrusion-based signalling has the potential to yield robust self-organizing tissue-wide patterns without the need to invoke diffusion-mediated signalling.
© 2010 The Royal Society
Figures


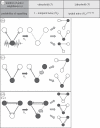

References
-
- Classen A. K., Anderson K. I., Marois E., Eaton S. 2005. Hexagonal packing of Drosophila wing epithelial cells by the planar cell polarity pathway. Dev. Cell 9, 805–81710.1016/j.devcel.2005.10.016 (doi:10.1016/j.devcel.2005.10.016) - DOI - DOI - PubMed
-
- Cohen M., Georgiou M., Stevenson N. L., Miodownik M., Baum B. 2010. Dynamic filopodia drive pattern refinement via intermittent N-Dl signalling. Dev. Cell 19, 78–8910.1016/j.devcel.2010.06.006 (doi:10.1016/j.devcel.2010.06.006) - DOI - DOI - PubMed
-
- Maini P. K., Baker R. E., Chuong C.-M. 2006. Developmental biology. The Turing model comes of molecular age. Science 314, 1397–139810.1126/science.1136396 (doi:10.1126/science.1136396) - DOI - DOI - PMC - PubMed
-
- Webb S. D., Owen M. R. 2004. Oscillations and patterns in spatially discrete models for developmental ligand-receptor interactions. J. Math. Biol. 48, 444–47610.1007/s00285-003-0247-1 (doi:10.1007/s00285-003-0247-1) - DOI - DOI - PubMed
-
- Amoyel M., Cheng Y. C., Jiang Y.-J., Wilkinson D. G. 2005. Wnt1 regulates neurogenesis and mediates lateral inhibition of boundary cell specification in the zebrafish hindbrain. Development 132, 775–78510.1242/dev.01616 (doi:10.1242/dev.01616) - DOI - DOI - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

