A geometrical model for DNA organization in bacteria
- PMID: 21085464
- PMCID: PMC2972204
- DOI: 10.1371/journal.pone.0013806
A geometrical model for DNA organization in bacteria
Abstract
Recent experimental studies have revealed that bacteria, such as C. crescentus, show a remarkable spatial ordering of their chromosome. A strong linear correlation has been found between the position of genes on the chromosomal map and their spatial position in the cellular volume. We show that this correlation can be explained by a purely geometrical model. Namely, self-avoidance of DNA, specific positioning of one or few DNA loci (such as origin or terminus) together with the action of DNA compaction proteins (that organize the chromosome into topological domains) are sufficient to get a linear arrangement of the chromosome along the cell axis. We develop a Monte-Carlo method that allows us to test our model numerically and to analyze the dependence of the spatial ordering on various physiologically relevant parameters. We show that the proposed geometrical ordering mechanism is robust and universal (i.e. does not depend on specific bacterial details). The geometrical mechanism should work in all bacteria that have compacted chromosomes with spatially fixed regions. We use our model to make specific and experimentally testable predictions about the spatial arrangement of the chromosome in mutants of C. crescentus and the growth-stage dependent ordering in E. coli.
Conflict of interest statement
Figures
 (which is twice the persistence length
(which is twice the persistence length  ). With this step size the directions of two sequential steps are completely uncorrelated. In the simplest picture the random walk may intersect itself, since the diameter of DNA is much smaller than the grid size.
). With this step size the directions of two sequential steps are completely uncorrelated. In the simplest picture the random walk may intersect itself, since the diameter of DNA is much smaller than the grid size.
 (corresponding to a volume of
(corresponding to a volume of  for
for  ). The position on the chromosome is parameterized by the contour length s (measured in units of DNA length L). (A) Walk of length 26000b representing the genome. Ori and ter lie on the cell axis at opposite poles. Their distance from the bottom and top cell walls is 0b (red curve) and 4b (green curve). Error bars represent the standard deviations between the different DNA configurations sampled in the 106 runs. Dots represent the experimental data from Ref. . (B) Same plot as in (A) but for different Kuhn lengths (
). The position on the chromosome is parameterized by the contour length s (measured in units of DNA length L). (A) Walk of length 26000b representing the genome. Ori and ter lie on the cell axis at opposite poles. Their distance from the bottom and top cell walls is 0b (red curve) and 4b (green curve). Error bars represent the standard deviations between the different DNA configurations sampled in the 106 runs. Dots represent the experimental data from Ref. . (B) Same plot as in (A) but for different Kuhn lengths ( ). DNA length and cell volume are kept constant. Here, the standard deviations between the individual realizations are rescaled and shown as function of the position on the chromosome.
). DNA length and cell volume are kept constant. Here, the standard deviations between the individual realizations are rescaled and shown as function of the position on the chromosome.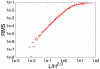
 with
with  . The square indicates the data point for L = 26000, H = 40 corresponding to the parameter values of C. crescentus.
. The square indicates the data point for L = 26000, H = 40 corresponding to the parameter values of C. crescentus.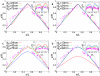
 and
and  where H is the length of the cell) have been adjusted to minimize the differences between experimental data and the predictions of the model. Figs. C and D are for the same blob parameters as A and B, respectively. However, in C and D only ori has a fixed position at
where H is the length of the cell) have been adjusted to minimize the differences between experimental data and the predictions of the model. Figs. C and D are for the same blob parameters as A and B, respectively. However, in C and D only ori has a fixed position at  , while ter is free to move. One should note that because of the additional freedom in moving ter the DNA configuration shows a different dependence on the blob size than with fixed ter.
, while ter is free to move. One should note that because of the additional freedom in moving ter the DNA configuration shows a different dependence on the blob size than with fixed ter.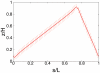
 . The chain consists of 2000 blobs: 1500 blobs for the segment connecting ori and ter and 500 blobs for the segment connecting ter and ori. Cell size is
. The chain consists of 2000 blobs: 1500 blobs for the segment connecting ori and ter and 500 blobs for the segment connecting ter and ori. Cell size is  . The error bars denote standard deviations from mean position.
. The error bars denote standard deviations from mean position.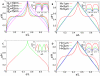
 and
and  ). The configurations shown in figure A are for a cellular volume of
). The configurations shown in figure A are for a cellular volume of  and different blob diameters by assuming a constant density of DNA of
and different blob diameters by assuming a constant density of DNA of  per blob. The dependence on the volume at constant DNA density is shown in figure B. Cell shapes are varied at constant cross section but different length
per blob. The dependence on the volume at constant DNA density is shown in figure B. Cell shapes are varied at constant cross section but different length  (corresponding to H = 33…165 blobs). The largest newborn cell has a volume of
(corresponding to H = 33…165 blobs). The largest newborn cell has a volume of  . Figure C shows a DNA configuration in a cell with two chromosomes (shown in different colors) just prior to cell division. The two ori have fixed positions at the cell poles, the two ter are kept at midcell. The contour length is measured along the path left (chromosome #1)-right (chromosome #2)-left (chromosome #2)-right (chromosome #1). Data shown are for a volume of
. Figure C shows a DNA configuration in a cell with two chromosomes (shown in different colors) just prior to cell division. The two ori have fixed positions at the cell poles, the two ter are kept at midcell. The contour length is measured along the path left (chromosome #1)-right (chromosome #2)-left (chromosome #2)-right (chromosome #1). Data shown are for a volume of  and each chromosome is represented by 2000 blobs. In this way the cellular DNA density remains constant and that the length of compacted DNA per blob (given by
and each chromosome is represented by 2000 blobs. In this way the cellular DNA density remains constant and that the length of compacted DNA per blob (given by  DNA per blob) is independent of the volume. A DNA configuration in these faster growing cells at an earlier stage of the cell cycle is shown in figure D. Here, the cell contains an additional DNA strand whose ends are anchored in the midplane of the cell mimicking the geometry of the chromosome after half the replication time [when the replication forks are located at 3 o'clock and 9 o'clock on the mother chromosome (solid lines)]. The presence of additional DNA makes the linear correlation stronger. For comparison the DNA configurations without daughter DNA are shown (dashed lines). Parameter values are as in figure B. The insets show the (rescaled) standard deviations from the mean configurations as function of s.
DNA per blob) is independent of the volume. A DNA configuration in these faster growing cells at an earlier stage of the cell cycle is shown in figure D. Here, the cell contains an additional DNA strand whose ends are anchored in the midplane of the cell mimicking the geometry of the chromosome after half the replication time [when the replication forks are located at 3 o'clock and 9 o'clock on the mother chromosome (solid lines)]. The presence of additional DNA makes the linear correlation stronger. For comparison the DNA configurations without daughter DNA are shown (dashed lines). Parameter values are as in figure B. The insets show the (rescaled) standard deviations from the mean configurations as function of s.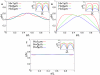
 , i.e. 33 to 165 blob diameters (with a blob diameter of
, i.e. 33 to 165 blob diameters (with a blob diameter of  ) at constant DNA density, i.e. the number of blobs is kept constant at 2000. In Fig. A ori and ter are positioned in midcell (
) at constant DNA density, i.e. the number of blobs is kept constant at 2000. In Fig. A ori and ter are positioned in midcell ( and
and  ), in Fig. B ori is at the cell pole and ter is positioned in midcell (
), in Fig. B ori is at the cell pole and ter is positioned in midcell ( and
and  ), and in Fig. C both ori and ter are in midcell (
), and in Fig. C both ori and ter are in midcell ( and
and  with
with  and
and  ). The insets show the (rescaled) standard deviations from the mean configurations as function of s.
). The insets show the (rescaled) standard deviations from the mean configurations as function of s.
 sites (representing a cellular volume of
sites (representing a cellular volume of  ). The lattice spacing is equal to the blob diameter
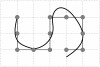
). The lattice spacing is equal to the blob diameter  . The chromosome then consists of 2000 blobs. The color coding represents the distance from ori and ter: gene positions close to ori are shown in red, gene positions close to ter are shown in blue. Intermediate regions on the ori to ter and on the ter to ori segment are shown in green.
. The chromosome then consists of 2000 blobs. The color coding represents the distance from ori and ter: gene positions close to ori are shown in red, gene positions close to ter are shown in blue. Intermediate regions on the ori to ter and on the ter to ori segment are shown in green.References
-
- Norris V. Hypothesis: chromosome separation in Escherichia coli involves autocatalytic gene expression, transertion and membrane-domain formation. Mol Microbiol. 1995;16:1051–1057. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

